Dividing Polynomials | Division of polynomials examples with solutions

Division of a polynomial by another polynomial is one of the important  concept in Polynomial expressions. In this article explained about  basic phenomena of diving polynomial algorithm in step by step process

Algebra division| Dividing Polynomials Long Division

Before going to algebra divisions observe the normal numerical division algorithm

When we divide 137 by 5 we get the quotient 27 and remainder 2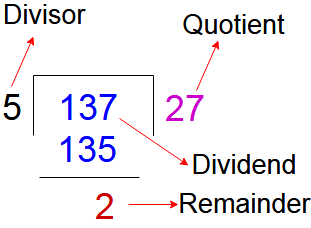

We can write 137 as

137 = (5 x 27) + 2   (Note : Here remainder 2 and it is less than divisor 5)

i.e Dividend = Divisor x Quotient + Remainder

The same division algorithm of number is also applicable for division algorithm of polynomials.

i.e When a polynomial divided by another polynomial

Dividend = Divisor x Quotient + Remainder, when remainder is zero or polynomial of degree less than that of divisor

A polynomial f(x) is divided by another polynomial g(x) we get quotient q(x) and remainder p(x) such that

f(x) = g(x) . q(x) + p(x)

Where p(x) = 0 or degree of p(x) < degree of g(x)

Polynomial long division examples with solution

Dividing polynomials by monomials

Take one example

Example -1 :  Divide the polynomial 2x⁴ +3x² +x  by x

Here 

= 2x³ + 3x +1

So we write the polynomial 2x⁴ +3x² +x as product of x and 2x³ + 3x +1

2x⁴ +3x² +x = (2x³ + 3x +1) x

It means x & 2x³ + 3x +1 are factors of 2x⁴ +3x² +x

Example – 2 : Divide the polynomial 3x³ + 9x² + 5 by 3x

Here variable “x” in denominator so it is not a polynomial.

So polynomial of 3x³ + 9x² + 5 can be written as

3x³ + 9x² + 5 = 3x (x² + 3x) +5

Here we can say (x² + 3x) is the quotient, 3x is the divisor and 5 is the remainder. And also we can say that the reminder is not zero, 3x is not a factor of 3x³ + 9x² + 5

Dividing Polynomials by Binomials

Example – 3: Divide the polynomial 4x²-3x +x³ +10 by x+4 and verify the remainder with zero of the divisor

Solution: Say f(x) = 4x²-3x +x³ +10  and g(x)= x+4

For this division, we have using the steps as follows

Step: 1 – Arrange the terms of the dividend f(x) and the divisor g(x) in descending order of their degree

f(x)= x³ +4x²-3x  +10 and g(x) = x+4

Step:2 – We get first term of quotient by dividing the first term of dividend (i.e  x³ ) with first term of divisor (i.e x)

So

Step:3 – Now the first term of quotient x² multiplying the divisor g(x) and that term subtract from dividend

x² (x +4) = x³ +4x²

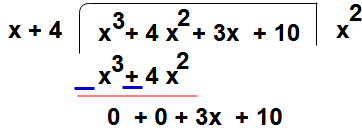
Step : 4 –  Now repeat the step 2 again

i.e  To get second term of quotient by dividing the first term of get remainder in previous step (i.e  3x ) with first term of divisor (i.e x)

So

Step:5 – Then second term of quotient 3 multiplying the divisor g(x) and that term subtract from remainder got in step 3

3(x +4) = 3x + 12

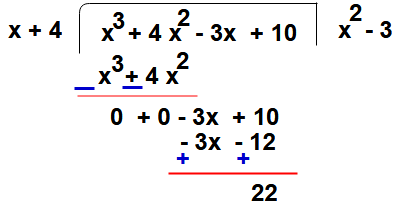
Here the quotient is (x² – 3) and remainder is 22

Here we can write this division process as

Dividend = Divisor x Quotient + Remainder

f(x)  = (x² – 3) g(x) + 22

x³ +4x²-3x  +10 =  (x² – 3) ( x+4) + 22

By using the remainder theorem we obtaining the remainder  without performing the above process

Note : Remainder theorem applicable only for divisor have linear polynomial with one variable

Consider zero of the polynomial of g(x) is   – 4

g(x) = x +4

g(-4) = -4 +4 = 0

Now find the value of f(x) at x= -4

f(4) = 4 (-4)² – 3(-4) + (-4)³ + 10 = 22

Dividing Polynomials by Trinomials

Example  -4: Divide the polynomial  5x⁵  + x²  + 3x³ –  4x⁴– 10  by  2 +  x² – x

Solution:  Say f(x) = 5x⁵  + x²  + 3x³ –  4x⁴– 10 and g(x)= 2 +  x² – x

Now divide f(x) by g(x) by the following steps

Step: 1 – Arrange the terms of the dividend f(x) and the divisor g(x) in descending order of their degree

f(x)= 5x⁵  – 4x⁴  + 3x³  + x² – 10  and g(x) = x² – x  + 2

Step:2 – We get first term of quotient by dividing the first term of dividend (i.e  5x⁵ ) with first term of divisor (i.e x²)

So 

Step : 3 – Now the first term of quotient 5x³ multiplying the divisor g(x) and that term subtract from dividend

5x³ (x² – x  + 2) = 5x³ – 5x⁴ + 10x³

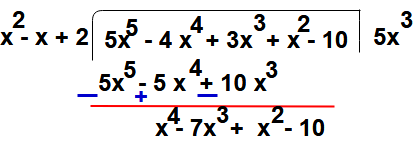
Step : 4 –  Now repeat the step 2 again

i.e  To get second term of quotient by dividing the first term of get remainder in previous step (i.e  x⁴ ) with first term of divisor (i.e x²)

So 

Step:5 – Then second term of quotient x² multiplying the divisor g(x) and that term subtract from remainder got in step 3

x² (x² – x  + 2) = x⁴ – x³  + 2x²

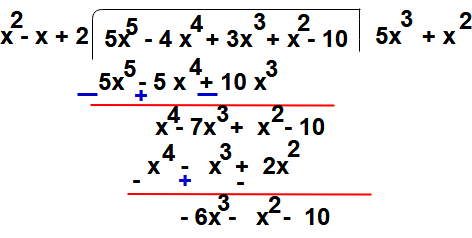
Step : 6 –  Now repeat the step 4 again

i.e  To get third term of quotient by dividing the first term of get remainder in previous step (i.e  -6x³ ) with first term of divisor (i.e x²)

So 

Step:7 – Then third term of quotient -6x multiplying the divisor g(x) and that term subtract from remainder got in step 5

-6x (x² – x  + 2) = -6x³  + 6x²  – 12x

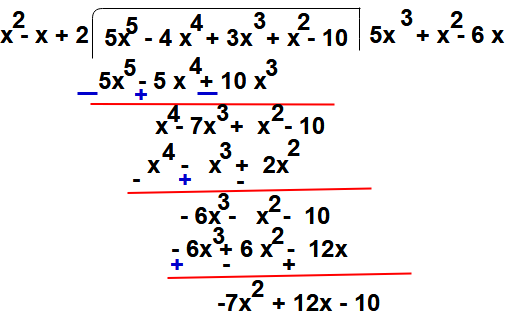
Step : 8 –  Now repeat the step 6 again

i.e  To get forth term of quotient by dividing the first term of get remainder in previous step (i.e  -7x² ) with first term of divisor (i.e x²)

So 

Step:9 – Then forth term of quotient -7 multiplying the divisor g(x) and that term subtract from remainder got in step 7

-7 (x² – x  + 2) = -7x²  + 7x  – 14

Here the division process is completed because degree of (5x + 4)  = 1 which is less than the degree of the divisor (x² – x  + 2)

So the quotient is (5x³  + x³  -6x – 7) and remainder is 5x + 4

Here we can write this division process as

Dividend = Divisor x Quotient + Remainder

f(x)  =  (5x³  + x³  -6x – 7) g(x) + ( 5x + 4)

(5x⁵  + x²  + 3x³ –  4x⁴– 10)  =  (5x³  + x³  -6x – 7)  (x² – x  + 2)  + ( 5x + 4)

Dividing Polynomials by Quadratics

Example: Divide the polynomial   1 + x  + 5x⁵  -4x⁴  + 3x³ – 2x²  by  2 + x +  x²  + x³

Solution:  Say f(x) = 1 + x  + 5x⁵  -4x⁴  + 3x³ – 2x²  and g(x)= 2 + x +  x²  + x³

Now divide f(x) by g(x) by the following steps

Step: 1 – Arrange the terms of the dividend f(x) and the divisor g(x) in descending order of their degree

f(x)= 5x⁵  -4x⁴  + 3x³ – 2x² + x +1   and g(x) = x³ +  x²  + x + 2

Step:2 – We get first term of quotient by dividing the first term of dividend (i.e  5x⁵ ) with first term of divisor (i.e x³)

So  

Step:3 – Now the first term of quotient 5x² multiplying the divisor g(x) and that term subtract from dividend

5x² (x³ +  x²  + x + 2) = 5x⁵ + 5x⁴ + 5x³  +  10x²

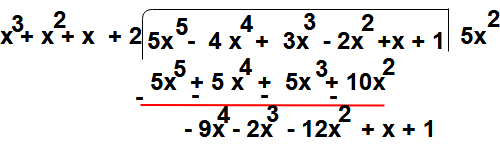
Step : 4 –  Now repeat the step 2 again

i.e  To get second term of quotient by dividing the first term of get remainder in previous step (i.e  -9x⁴ ) with first term of divisor (i.e x³)

So 

Step:5 – Then second term of quotient -9x multiplying the divisor g(x) and that term subtract from remainder got in step 3

-9x  (x³ +  x²  + x + 2)  = -9x⁴ – 9x³  – 9x²  – 18x

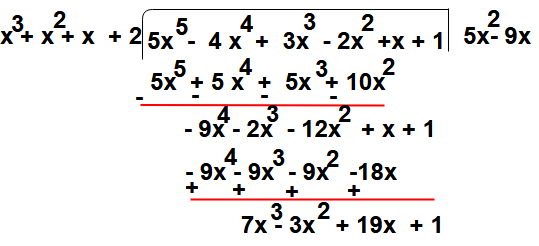
Step : 6 –  Now repeat the step 4 again

i.e  To get third term of quotient by dividing the first term of get remainder in previous step (i.e  7x³ ) with first term of divisor (i.e x³)

So 

Step:7 – Then third term of quotient  7  multiplying the divisor g(x) and that term subtract from remainder got in step 5

7 (x³ +  x²  + x + 2) = 7x³ + 7 x²  + 7x + 14

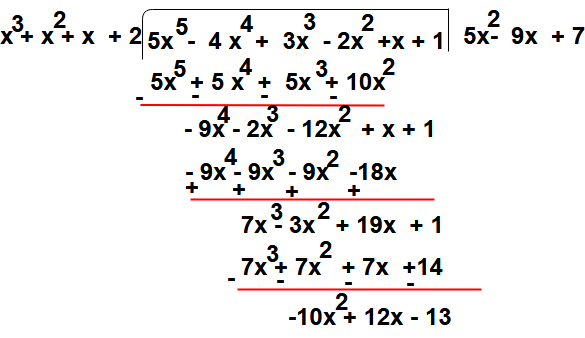
Here the division process is completed because degree of (- 10x² + 12x  -13 )  = 2 which is less than the degree of the divisor (x³ +  x²  + x + 2)

So the quotient is (5x²  -9x  + 7) and remainder is  -10x²  + 12x  -13

Here we can write this division process as

Dividend = Divisor x Quotient + Remainder

f(x)  =   (5x²  -9x  + 7) g(x) + ( -10x²  + 12x  -13 )

(5x⁵  -4x⁴  + 3x³ – 2x² + x +1) =   (5x²  -9x  + 7) (x³ +  x²  + x + 2) + ( -10x²  + 12x  -13 )

I Hope you liked this article  about division of polynomials examples with solutions. Give feed back, comments and please don’t forget to share it.

Related Topics

Polynomial Basic Concepts | Types of polynomials | Algebraic Expressions

Remainder and Factor Theorem Proof | Remainder and Factor Theorem Test

Remainder Theorem Tough Questions for Competitive Exams | Aptitude Questions