Questions and Answers on Profit and Loss Chapter | Exercise – 4
In Profit and Loss Exercise – I Covered the terminology with exercise sums on Cost Price (CP), Selling price (SP), Profit percent/Gain percent & Loss percent.
In Profit and Loss Exercise – II Covered the terminology with exercise sums on Mark Up, Marked price/ List Price, Discount, Discount Percentage & Successive discounts.
In Profit and Loss Exercise – III Covered the terminology with exercise sums on Direct Cost, Indirect Cost, Break Even Point, Faulty Measure or Faulty Balances.. etc
Now In this exercise given Questions and Answers on Profit and Loss chapter summery of all concepts.
Example – 1 : Naveen Purchased a cycle at cost of ₹2000 and it sold Ram at 20% profit. Now Ram spent ₹100 for its repair and sold to Jhon at 10% loss. Find the Cost price of Jhon?
Answer: The Cost Price of Naveen = 2000
Sell price of Naveen = 20% profit on 2000
= 2000 x 120 / 100 = 2400
Ram cost price = 2400 + 100 = 2500 (because Ram spent ₹ 100 for its repair )
Sell price of Ram = 10% loss on 2500
= 2500 x 90 / 100 = 2250
The Cost price of Jhon = ₹ 2250
Example –2 : Jhon sells a article to Tom at a gain of . Tom sells it to Jhosi at a loss of 2 and Jhosi again sells it to Phani at a profit of If Phani pays to Tom, what is the cost price of the article for Jhon?
Answer : Here take X= +20 , Y = -25, & Z = 20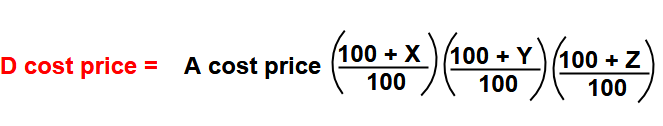
Phani cost price ( 1728 ) = Jhon cost price x ( 120 / 100) x (75 / 100)x ( 120 / 100)
Jhon cost price = 1728 x ( 100 / 120) x (100/75) x (100 / 120) = 1600
Jhon cost price =
Example – 3 : The Cost price of the two articles were same and they sold one at 25% profit and another sold at 20% loss. Now find the overall profit/ loss in this transaction?
Answer : One simple formula while at same cost price
Net profit / loss percent = ( x + y ) / 2
Here to be take ” +ve” sign for profit and “-ve ” sign for Loss & same rule also applicable for final answer.
So x = 25 & y = -20
= ( 25 – 20) / 2 = + 2.5%
Profit = 2.5%
Example – 4 : A person sells two articles at the same price, one at a profit of and another at a Loss of
Answer : For this type of sums we used the below formula ( while at same selling price)
Here to be take ” +ve” sign for profit and “-ve ” sign for Loss & same rule also applicable for final answer.
So x = 25% and y = – 30%
=[ ( 100 x -5 ) – 1500 ] / 195
= -2000 / 195 = – 400 / 39 ( – ve sign means it is Loss )
Example -5 : A shopkeeper sells 20% articles at 20% profit and he sells 30% of remaining articles at 25% loss. Now remaining two articles sold at 50% profit.
Answer : Here Take articles = 100 and Cost Price = 100
Transaction – 1 – Sells 20% articles at 20% profit
= 20 x 120 / 100 = 24
Transaction – 2 – Sells 30% of remaining articles at 25% loss.
So 30% of remaining articles means 30% of 80
= 80 x 30 / 100 = 24 articles at 25 % loss
=24 x (75 / 100)
= 18
Transaction – 3 – Remaining Sold at 50% profit.
Remaining articles 56 (=100 – 20 – 24) sold at 50% profit
= 56 x 150 / 100 = 84.
The total sold price of 100 articles = 24 + 18 + 84 = 126
So In this overall transaction the shopkeeper got 26% profit.
Example – 6 : A shopkeeper offer successive discounts 60% , 20% & 20% on product. Now find the overall discount on that product
Answer : Here take d1 = 60% , d2 = 20% & d3 = 20% and use this in following formulas
![]() = 100 – [ 100 x (40 /100 ) x ( 80/100) x ( 80 /100) ]
= 100 – [ 100 x (40 /100 ) x ( 80/100) x ( 80 /100) ]
= 100 – 25.6
= 74.4 %
Overall Discount = 74.4 %
Example – 7 : A company sells two goods for 24000 each. One it gained 25% and on the other it lost 25%. What is the overall gain or loss percent?
Answer :
Hint: If SP of two articles is same such that there is x% gain on one and x% loss on the other then there will be always a loss of ( x / 10 )2.
So here x = 25
= (25 / 10 )2
= 625 / 100 = 6.25%
Loss percent = 6.25%.
Example – 8 : A Shopkeeper marks his goods 20% above the cost price , but allows a discount of 10% on the marked price. What is the gain or loss% in the deal for the shopkeeper?
Answer:
Hint : If there is two successive changes x% and y% then overall change in percent
Here to be take “-ve” sign for loss/ discounts and +ve sign for profit / mark up and finally the value comes ” +ve ” then it gives profit and the values comes ” -ve ” value then it incurred Loss.
sao x = + 20 , y = – 10
% of profit / Loss = 20 – 10 – ( 200 / 100) = + 8%
Profit percent = 8%.
Example – 9 : A Shopkeeper even after allowing a discount of 20% , he still gets a profit of 30% on the article. Then find mark up percent of that article ?
Answer: Here also using the above formula
30 = x – 20 – (20x / 100)
50 = 0.8 x
x = 500/8 = 62.5
Marked percent of the article = 62.5%
Example – 10 : A fruits vender cost price of apples is equal to selling price of apples, what is the profit/loss percentage?
Answer : Here using the following formula
If cost price of “ “objects is same as selling price of “ objects, profit / loss percentage
[ ( x – y ) 100 ] / y
Now x = 20 and y = 15
Profit / loss percent = [ ( 20 – 16) 100 ] / 16 = 400/16 = + 25% ( “+ve sig means profit and -ve sign means loss)
Profit percent = 25%
Example – 11 : A trader sells his product at loss and he uses less weight. Find his overall profit/loss percentage.
Answer : Take m = 100 , (m – t) = 25 , P = -20 , t = 75 , (100% – 25%)
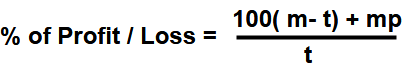 Profit /loss % = ( 100 x 25 – 20 x 100 ) / 75 = 500 / 75 = 20 /3
Profit /loss % = ( 100 x 25 – 20 x 100 ) / 75 = 500 / 75 = 20 /3
![]()
Quantitative Aptitude Main Page

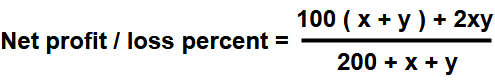
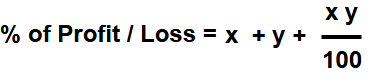






2 thoughts on “Profit and Loss Problems and Solutions for all Competitive Exams”
vinay
(November 4, 2018 - 3:05 pm)Can you please chick example 6 (near 200+x+y), According to given values x=25,y=-30 so (200+25-30 = 195) its not 255
sivaalluri
(November 6, 2018 - 3:49 pm)Thank you for your valuable correction