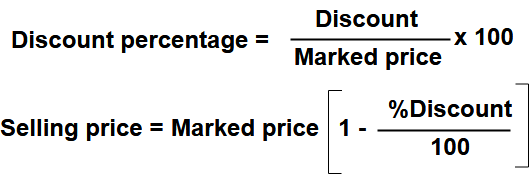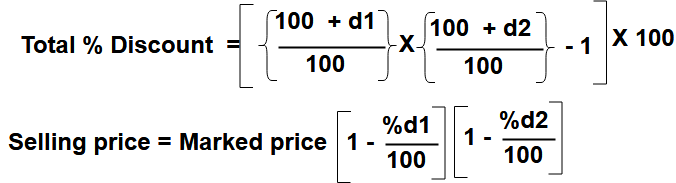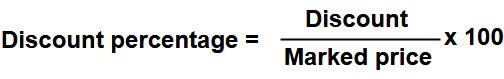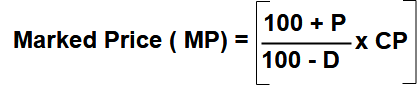Profit and Loss Formulas | Quantitative Aptitude Questions and Answers

Formulas for Profit and loss and practice sums | Exercise – 2

In Profit and Loss Exercise – 1 explained about the terminology of Cost Price (CP), Selling price (SP), Profit (P), Loss(L), Profit percent, Loss percent, Gain , Gain percent with formulas and practice sums.

In This Chapter explained the following terminology definitions with formulas and examples.

Mark Up, Marked price,
Discounts, Successive discounts,
Variable cost, Fixed cost,
Break even point,
Faulty balances, faulty measure , Chain rules

Mark Up

The manufacturer/trader/businessmen, while selling goods, add a certain percentage on the cost price (CP). This addition is called percentage mark up.

Marked price/ List Price

The mark up is in terms of price then obtained marked price.

i.e the price on the label of an article is called its marked price or list price

List price or the tag price is the price that is printed on the tag of the article or good for selling

CP + Mark Up = Marked price.

CP + % Mark Up on CP = Marked Price.

Selling Price = Marked price ( If not having any discount)

Profit % = [ ( M.P – C.P ) x 100 ] / C.P ( If not having discount )

Discount

The deduction on the marked price is called discount. If manufacturer/trader/businessmen, gives discount, he does so on the marked price and after the discount is sold at its discounted price.

Selling Price = Marked Price – Discount.

Discount = Marked Price – Selling Price

Discount Percentage

The percentage reduction for selling the article on marked price.

i.e Discount percentage expressed as a percent of marked price.

Successive discounts

For discount d1% and d2%, successive discount, then

After D% discount, requires P% profit, then total cost price increased in percent

If CP of two articles are same, and they sold at

1 . Profit x% for 1st article and Profit y% for 2nd article then overall profit %

Profit % = (x + y ) /2

2 . Profit x% for 1st article and Loss y% for 2nd article then overall profit % or Loss %

Profit % = (x – y ) /2 ( If x > y )

Loss % = ( y – x ) /2 ( If y > x )

3 . Loss x% for 1st article and Loss y% for 2nd article then overall Loss %

Loss % = (x + y ) /2

4 . Loss x% for 1st article and profit x% for 2nd article then overall No profit, No loss

If SP of two articles are same and they sold at x% Loss for 1st article and x% profit for 2nd article then overall got loss.

Loss % = ( x² /100).

Practice Sums related to above profit and loss formulas

Example – 1 : A shop keeper purchases two pens at ‎₹500 each. He sold one pen at 10% gain and the other at 10% loss. What is the total gain or loss percentage?

Answer : Here Cost price for both pens were same so according to above formulas there is NO profit and No loss for this transaction.

1^st pen selling price ( SP ) = 500 x 1.1 = 550 ( 10% profit = 110/ 100 = 1.1 )

2^st pen selling price ( SP ) = 500 x 0.9 = 450 ( 10% Loss = 90/ 100 = 0.9 )

Cost price of both pens ₹ 1000 = Sell price of both pens ₹1000.

Example – 2 : A Trader sells two laptops for 24000 each. One he gained 20% and other he incurred loss 20%. What is the gain or loss percentage?

Answer : Here Sell price for both laptops were same so according to above formulas finally got loss &

Loss % = ( x² /100). here x = 20

Loss = 20 x 20 / 100 = 400 / 100 = 4%.

Example – 3 : A Shop Keeper bought two articles for ‎₹ 900. He sold one article at a profit 20% and the other at a loss of 4% and he found each article was sold at the same valve. What is the cost price of the article sold at a loss?

Answer : Here Cost price of both articles not same but sold price is the same.

And required cost price of article which is sold at loss so it is to be take ” X “.

CP of both articles are ” X ” & ” 900 – X “

Sold price of the articles are 0.96X & 1.2(900 – X) respectively. [ Since 4% loss for X and 20% profit for (900 -X) ]

In this sum given both articles sold at same price. So

0.96X = 1.2( 900 – X)

2.16 X = 1080

X = 1080 / 2.16 = 500.

The cost price of the article sold at a loss is ‎₹500.

Example – 4 : A trader marked his goods 20% above the cost price, but allows a discount of 10% on the marked price. What is the profit or loss% in this transaction for the trader.

Answer : Take Cost price = CP then

Marked price = 1.2 CP ( Since 20% extra on CP )

Selling Price ( SP)= 1.2 CP [ 1 – (10/100) ] = ( 1.2 x 0.9) CP = 1.08 CP

SP/ CP = 108 /100

Profit % = 8%

Example – 5 : After getting two successive discounts of 20% and 10% , customer purchased a good for 432. What is the list price of the good?

Answer : Here

Customer purchased price = Trader sold price. So

SP = 432 , d1 = 20 , d2 = 10

432 = MP x ( 80 / 100) x (90 /100)

MP = (432 x 100) / (8 x 9) = 600

The good marked or listed price = ₹600.

Example – 6 : An article listed at ₹ 500 with a discount of 10%. What additional discounts much be offered to the costumer to bring the net price to ₹423?

Answer: List price = ₹500

Selling price = 500 x (100 – % discount) %

= 500 ( 100 – 10) /100 = 500 x 0.9 = 450.

Again customer getting discount ₹27 (450-423) and purchased price was ₹426. Now take marked price as ₹450.

Discount percentage = ( 27 / 450 ) x 100 = 270 / 45 = 6 %.

Example – 7 : A person buys a cycle with 20% discount on its marked price. He makes a profit of 10% by selling it at ₹ 2200. Find its marked price.

Answer: Take the marked price = M.

The person cost price = 80% on M ( since he got 20% discount ).

= 0.8 x M

He selling at 10% profit his cost price

i.e selling price = 2200 = 1.1 ( 0.8 x M )

M = 22000 x ( 8x 11 ) = 20000/ 8 = 2500.

Marked price = ₹ 2500

Example – 8 : A shopkeeper mixed 26kg of rice at ₹20 per kg with 30 kg of rice of other variety at ₹36 per kg and sells the mixture at ₹30 per kg. Find his profit percent?

Answer : Cost price of total mixed rice ( 26kg + 30kg = 56 kg )

= 26 x 20 + 30 x 36

= 520 + 1080 = 1600

Sell Price of mixed rice = 30 x 56 = 1680

Profit = 1680 – 1600 = 80

% profit = ( 80 / 1600 ) x 100 = 5%

Example – 9 : A businessmen allows a discount of 10% on the marked price of a good. How much percentage above the cost price the good be marked to make a profit of 17%?

Answer: Here Discount d = 10% and profit required p =17%.

Use this formula

MP =[ (100+17)/(100-10)] x CP

MP/ CP = 117 / 90

MP/CP = 1.3

MP/CP = 130/100

So Marked price 30% more then cost price

Example – 10 : A trader sells two articles at the same price . He gets a profit 25% on one article and loss 20% on other article. Find his profit or loss recent in the whole transaction.

Answer : Here take profit x = 25% and loss y = 20% then using this below profit and loss formula