Types of Quadrilateral | Quadrilateral formula for area and perimeter

Quadrilateral Properties | Trapezium, parallelogram, Rhombus

What is Quadrilaterals

A Quadrilaterals is defined as a simple closed figure bounded by four lines in plane. If any four points are not colliner, then we obtain a closed figure.

There above all types of figures are know as quadrilaterals. We can easily draw many more quadrilaterals and we can identify many around us.

Terminology related to Quadrilaterals :

Sides and adjacent sides :

The four line segments AB, BC, CD & DA are known as sides of quadrilateral. Two sides of quadrilaterals which have a common end point are called the adjacent sides.

Thus ( AB, BC)  ; ( BC , CD )  ;  ( CD , DA ) ; ( DA , AB  ) are four pairs of adjacent sides of the quadrilateral of ABCD.

Vertices of the quadrilateral :

The points A, B, C & D are the Vertices of the quadrilateral ABCD.

Angles and adjacent sides :

The four angles ∠DAB , ∠ABC, ∠BCD & ∠CDA are known as angles of quadrilateral.  These angles can be also denoted as ∠A , ∠B, ∠C & ∠D respectively.

Two angles of the a quadrilateral having a common side are called its adjacent angles. Thus (∠A , ∠B ) ;  ( ∠B, ∠C ) ; (∠C , ∠D ) ; ( ∠D, ∠A) are four pairs of adjacent angles of the quadrilateral of ABCD.

Two angles of a quadrilateral which are not adjacent angles are the opposite angles . Thus (∠A , ∠C ) ;  ( ∠B, ∠D ) are two pairs of opposite angles of the quadrilateral of ABCD.

Diagonals of the quadrilateral:

The line segment joining the opposite vertices of a quadrilateral is called a Diagonals of the quadrilateral.

Here AC and BD are two diagonals of the quadrilateral ABCD.

Perimeter of the quadrilateral:

Quadrilateral perimeter mean, The sum of length of all the four sides of quadrilateral.

Here Perimeter of the quadrilateral ABCD = AB + BC + CD + DA.

Types of quadrilaterals with formulas :

Properties and formulas of Trapezium (Trapezoid) :

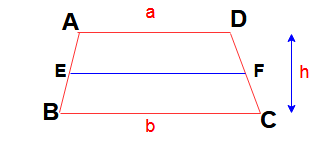
The quadrilateral having one pair of opposite sides parallel to each other is called a trapezium.

Here AD || BC ,  Height from base AD to base BC is ” h”  and length of AD = a and BC = b

Area of the trapezoid = 1/2 x sum of parallel sides x height

 Area of  Trapezium (Trapezoid)  ABCD = (1/2 ) (a + b) h.

1. If the non -parallel sides are equal then diagonals will be too.
2. Median of trapezium = 1/2  x sum of parallel sides ( median is the line equidistant from the parallel sides). Here EF is median of trapezium ABCD .  EF = (a + b) /2. (here AE = EB & DF= FC).

Isosceles trapezium :

The quadrilateral having one pair of opposite sides parallel to each other and other pair of sides are equal then it is called an Isosceles trapezium.

Parallelogram Properties and formulas:

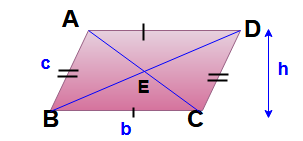
If both pairs of opposite sides of the quadrilateral  are parallel, such a quadrilateral is called parallelogram.

Area of  parallelogram = Base x height =  bh

Perimeter of  parallelogram = 2 ( b+ c )

Area of parallelogram = product of any two adjacent sides x sine of the included angle = b x c x sin B.

1. The opposite sides of a parallelogram are equal in length. Thus AB = DC and AD = BC.
2. Opposite angles of a parallelogram are congruent (equal measure).
3. The diagonals of a parallelogram bisect each other. Here BE = ED and AE = EC.
4. Each diagonal of a parallelogram divides it into two triangles of the same area. Here area of  ΔABC = Area of ΔACD and area of ΔABD = area of ΔBCD.
5. Bisectors of the angles of parallelogram form a rectangle.
6. A parallelogram inscribed in circle is a rectangle.
7. A parallelogram circumradius about a circle is a rhombus.
8. The sum of the squares of the diagonals is equal to the sum of the square of the four sides.
9. Here AC² + BD² = AB² + BC² + CD² + DA² = 2 b² + 2 c²

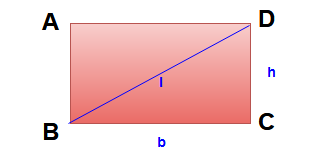
Properties and formulas of Rectangle:

A parallelogram having any one of its angle as right angle ( 90°) is a rectangle.

 

Area of the rectangle =  bh

Perimeter of the rectangle = 2 (b + h)

Length of diagonal  ( l )   = √ b² + h²

 

1. The diagonals of a rectangle are equal and bisect each other.
2. The opposite sides of a rectangle are parallel and opposite sides of a rectangle are congruent. Here AD || BC and AB || DC.
3. All four angles of a rectangle are right angles. Here ∠A =∠B = ∠C = ∠D =  90°.
4. All rectangles are parallelograms but the reverse is not possible.

Properties and formulas of Rhombus:

A parallelogram having equal adjacent sides is called a rhombus. 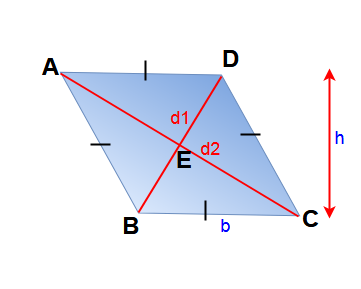Here $h=$ height,   AB = BC = CD = DA = b & AB || DC , AD || BC and   $d1,d2$ are the diagonals

Area of the Rhombus = 1/2 x product of diagonals x sine of the angle between them.

Area of the Rhombus ABCD = (1/2) d1 d2 ( Diagonals are right angle so sin 90° = 1)

Here Area of the Rhombus ABCD = bh

Perimeter of rhombus = 4b

1. All the sides of a rhombus are congruent. Here AB = BC = CD = DA = b.
2. Opposite sides of a rhombus are parallel. Here AB || DC  & AD || BC.
3. The diagonals of a rhombus bisect each other at right angles. Here ∠AED = ∠AEB = ∠BEC = ∠DEC = 90°.
4. Opposite internal angles of a rhombus are congruent (equal in size). Here ∠ABC  =  ∠ADC and ∠BAD = ∠DCB.
5. The sum of any two consecutive internal angles of a rhombus equal to 180°. Here ∠A + ∠B = ∠B + ∠C = ∠C +∠D = ∠D + ∠A = 180°.
6. All rhombuses are parallelograms but the reverse is not possible.
7. A rhombus may or may not be a square but all square but all squares are rhombuses.

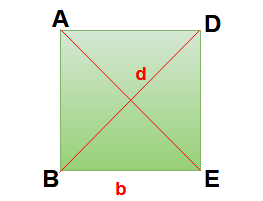
Properties and formulas of Square :

A parallelogram having equal adjacent sides and all angles of  right angle (90°) is called square.

Here length of the side for square ABCD = a

Length of diagonal = d = √2  a

Area of the square = b²

Area of the square ABCD = (1/2) d²

Perimeter of the square = 4b

 

1. All four sides of a square are congruent.
2. Opposite sides of a square are parallel. Here AB || DC  & AD || BC.
3. The diagonals of a square are equal. Here AE = BD
4. The diagonals of a square bisect each other at right angles. Here ∠AED = ∠AEB = ∠BEC = ∠DEC = 90°.
5. All angles of a square are 90° . Here ∠A = ∠B = ∠C  = ∠D = 90°.
6. All squares are belongs to  a special kind of rectangles where all the sides have equal length.
7. Side is the diameter of the inscribed circle.
8. Diagonal is the diameter of the circumradius circle. Here Diameter = √2  a & circumradius = a / √2 

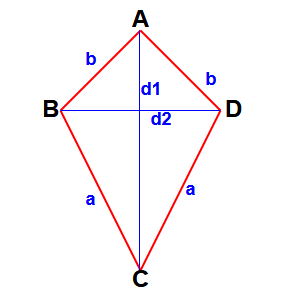
Area of Kite:

The quadrilateral having two pairs of equal adjacent sides is called kite.

Here BC = DC = a & AB = AD = b

d1 is the length of a diagonal.

d2 is the length of the other diagonal.

Area of kite = (1/2) d1 d2.

 

 

 

 

Some Important points in quadrilaterals

1. Parallelograms, trapeziums, rhombuses, rectangles and squares are all quadrilaterals.
2. Parallelograms, rhombuses, rectangles and squares are all trapeziums.
3. Rhombuses, rectangles and squares are all Parallelograms.
4. All squares are Rhombuses but the converse is not true.
5. all squares , rhombuses are kites.

Classifications of Triangles with properties | Triangle Area Formulas

Hi friends Thanks for reading. I Hope you liked it. Give feed back, comments and please don’t forget to share it.