Remainder Theorem for Number System | Remainder Theorem Difficult Examples

Remainder Theorem of Numbers | Remainder Problems in Aptitude

Before going to concepts of remainder theorem of numbers, it is better to understand the the concepts of  Divisor, Dividend, Quotient and Remainder

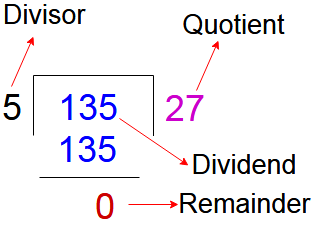
Remainder Theorem Rule – 1 (Fundamental)

Remainder  of the  expression can be expressed as positive remainders and negative remainders. Technically both positive and negative remainders are correct.

But remainders by definition are always non-negative. So final answer to be expressed in positive value only. For simplification of solution take negative remainder and finally it is to be convert into positive remainders.

Note:

• Add divisor to negative remainder then it will gives positive remainder
• Subtract positive remainder from divisor then it will gives negative remainder

Example – 1 :  Find the remainder of the expression of 49 / 9

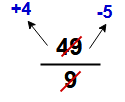
In this question

Positive remainder =  +4

Negative remainder  = -5

As per the remainder theorem the final answer is   “4 “

Example – 2 :  Find the remainder of the expression of 107 / 9

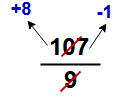
In this question

Positive remainder =  +8

Negative remainder  = -1

In this expression finding the negative remainder is very easy when compare to positive remainder.

So take negative remainder “-1″ and add to it divisor ” 9″ then gives final answer = – 1 + 9  = 8

Remainder Theorem Rule – 2 (For long expressions)

The remainder of the expression      will be the same as the remainder of the expression

Where

A_R is the remainder when “A”  is divided by ” N”

B_R is the remainder when “B”  is divided by ” N”

C_R is the remainder when “C”  is divided by ” N”

D_R is the remainder when “D”  is divided by ” N”

Example – 3 :  Find the remainder  when 47 x 52 is divided by 6

Solution: 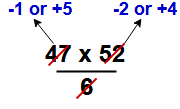Here remainder for 47/6  is -1 or 5  and  52/6  is -2 or 4

Case – 1 : -1 x -2 = 2/ 6     remainder = 2

Case – 2 : –1 x 4  = -4 / 6     remainder = – 4 + 6 (add divisor) = 2

Case-3 : 5 x -2  = -10 / 6     remainder = – 4 + 6 (add divisor) = 2

Case – 4 : 5 x 4  = 20 / 6     remainder =  2

As per the reduces the calculation we can choose the option

Remainder Theorem Rule – 3 (Cancellation rule)

For simplification of the expression of the sum, you should try to cancel out parts of the numerator and denominator as much as you can, then final remainder to be  multiplying the canceled number to get the correct remainder.

Example – 4 :   Find the remainder of 54 divided by 4.

= 54/4 = 27 / 2  ( cancel out by 2 of the numerator and denominator  )

Then remainder is of the final expression is 1

Final reminder for the given expression is = 1 x 2 = 2

Remainder Theorem Rule – 4 (remainder of a number with power )

There are two rules which are effect in order to deal with large powers

Case – 1 : If we can express the expression in the form , the remainder will become 1 directly.

In this case , there is no matter how large the value of the power “n” is, the remainder is 1.

Example – 5:  Find the remainder  when  (321)⁵⁶⁸⁷  is divided by 8

Solution: 321 can be expressed as [(8×40) + 1] so

remainder of the above question is (1)⁵⁶⁸⁷  = 1

Case – 2 : If we can express the expression in the form , the remainder will become ( – 1 )ⁿ

In this case , if n is even number then remainder will be 1 and if n is odd number then remainder will be (q-1)

Example – 6 :  Find the remainder  when  (146)⁵⁶  is divided by 7

Solution: 146 can be expressed as [(7×21) – 1] so

Remainder of the above question is (- 1)⁵⁶  = 1

Example – 7 :  Find the remainder  when  (269)⁵⁷⁵⁸⁷  is divided by 6

Solution: 269 can be expressed as [( 6x 45) – 1] so

Remainder of the above question is (- 1)⁵⁷⁵⁸⁷  =  – 1 = -1 + 6 = 5

Remainder theorem problems and solutions

Example – 8 : Find the remainder when 73 x 75 x 78 x 57 x 194 is divided by 25

Solution:

  = 0

Remainder theorem shortcut tricks : If denominator is perfectly divisible by any one number of given numerator expression values then remainder of the hole expression is Zero.

Example – 9 : Find the remainder when 84 + 98+ 197 + 240 + 140  is divided by 32

Solution:

 

So remainder of the above expression is 23

Example – 10 : Find the remainder when 1753 X 1749 X 83 X 171   is divided by 17

Solution: 

 

 So remainder of the above expression is 8

Example – 11 : Find the remainder when 3⁸⁵    is divided by 6

Solution:  Here 6 can be written as 3 x 2 so ( cancel out by 3 of the numerator and denominator )

Remainder is 1

Final remainder of the given question = 1 x 3 = 3

Example – 12 : Find the remainder when 2⁷⁰    is divided by 96

Solution:  Here 96 can be written as 2⁵ x 3 so ( cancel out by 2⁵ of the numerator and denominator )

Remainder is -1 + 3 = 2

Final remainder of the given question = 2 x  2⁵ = 2 x 32 = 64

Example – 13 : Find the remainder when 25¹⁰²    is divided by 17

Solution: Here 25 / 17  gives remainder is 8 so

Remainder of the sum is 4

For more sums on remainder theorem go through the below link

Remainder theorem hard problems with solutions

Topics in Quantitative aptitude math for all types of exams

Shortcut Math Tricks for helpful to improve speed in all calculations