In this session we know about basic concepts of logarithms like definition of logarithm with examples, common logarithms, natural logarithms and properties of logarithms.
Log Definition and Properties | logarithm tutorial | Exercise – 1
What is Logarithm
Take a relation between x, p and y is x = py
In the above relation, we are unable to decide the value of “y” for a given value of “x” because the relation may be the relative change does not follow the criteria of ratio or difference.
For example if you wont to get x = 25 in x = 5y, What should be the value of y?
Here power to which 5 must be raised to get 25 (i. e 5 x 5 = 25 & y = 2 )
Now defined the relation between “y” and “x”.
Here in 25 = 5y
“y” is called logarithm of 25 to the base 5 and it can be shortly written as log 5 25 = 2
Definition of Logarithm
Let “p” be a positive real number, p ≠ 0 and py = x. Then “y” is called the logarithm of “x” to the base “p” and is written as
log p x = y , and conversely if log p y = x then px = y
In logarithm equation of log p x = y, we can say that x >0 and p >o
( Since Logarithm to a negative base is not taken)
y = log p x is called the logarithm form and py = x is called the exponential form of the equation connecting p , y & x.
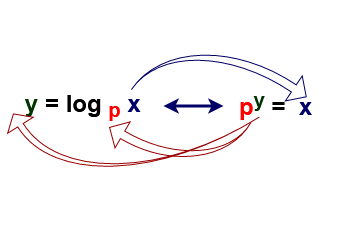
Some examples of exponential forms and their logarithmic forms
1 . Exponential form – a y = N
Logarithmic form – log a N = y
2 . Exponential form – 2 4 = 16
Logarithmic form – log 2 16 = 4
3 . Exponential form – 10 -2 = 0.01
Logarithmic form – log 10 0.01 = -2 =
4 . Exponential form – 3 -3 = 1/27
Logarithmic form – log 3 (1/27) = -3 =
Some Examples on logarithms
Example – 1 : Find how many 3s required to multiply for getting 27?
Answer: To get 27 , we have to multiply 3 of the 3s to get 27 ( i. e 3 x 3 x 3 = 27 )
So the logarithm is 3
Now we have to multiply 3 times the number 3 to get 27 is 3″ i.e log3 (27) = 3 &
read it as “logarithm of 27 to the base 3 is 3” or “log base 3 of 27 is 3”
Example – 2 : Find the value of log 4 1024
Answer: Here we have to multiply 5 times of the number 5 to get 1024 ( i.e 4 x 4 x 4 x 4 x 4 = 1024 )
So “logarithm of 1024 to the base 4 is 5 ” or “log base 4 of 1024 is 5
i.e log 4 1024 = 5
Example – 3 : Find the value of log 81 (3)
Answer: Let log 81 (3) = x
Exponential form – 81 x = 3 ⇔ (3 4) x = ( 3 ) 1
No According to exponential rules 4x = 1 ⇒ x = 1/4
Example – 4 : Find the value of log 2/3 (8/27)
Answer: Let log 2/3 (8/27) = x
Exponential form – (2/3) x = 8/27 ⇔ (2/3) x = ( 2/3 ) 3
No According to exponential rules x = 3
Characteristic and Mantissa
The logarithm of a number consists of two parts – One is an integral part and another is a decimal part.
The integral part of the logarithm of a number is called its characteristic and the decimal part is called mantissa
For example, log 10 25 = 1.3979
Here, Characteristic = 1 & Mantissa = 0.3979
Note: Mantissa is always written as a positive number.
Rule for writing Mantissa and Characteristic:
To make the mantissa positive ( In case the value of the logarithm of a number is negative), subtract 1 from the integral part and add to the decimal part.
For example log 10 (0.5) = – 0.3010
Thus – 0.3010 = – ( 0 + 0.3010 ) = – 0 – 0.3010 = – 0 – 1 + ( 1 – 0.3010) = – 1 + 0.699
So here mantissa is 0.699
When the characteristic is negative, it is represented by a bar on the number.
Thus in the above example instead of -1, we write
For the number of log base 10
If the number of digits in a number is ” n” then the characteristic of the logarithm of the number is ( n- 1)
If the characteristic of the logarithm of a number is “ n” then the number of digits in the number is ( n+1)
Note:
1. The characteristic of common logarithms of any positive number less than 1 is negative.
2. The characteristic of common logarithms of any positive number greater than 1 is positive.
3. If the logarithm to any base ‘ a ‘ given the characteristic ‘n ‘, then we can say that the number of integers possible is given by a n+1 – a n
Common Logarithms
Logarithms to the base “10” are called common logarithm. It is denoted as log 10 x simply denoted as log x
i. e while a logarithm is written without a base then it means the base is really 10
Natural Logarithm
Logarithms to the base ” e” are called natural logarithm. It is denoted as log e x
Here “e” is a constant, which is an irrational number with an infinite, non-terminating value of e = 2.718
Properties of Logarithm
1. log a 1 = 0 for a > 0 , a ≠ 1 ( i.e Log 1 to any base is Zero)
Proof: Let log a 1 = x . Then according to the logarithm definition
ax = 1 , so it is possible only if x = 0
Therefore ax = a 0 ⇔ x = 0.
Hence log a 1 = 0 for all a > 0 , a ≠ 1
2. log a a = 1 for a > 0 , a ≠ 1 ( i.e Log of a number to the same base is 1)
Proof : Let log a a = x . Then according to the logarithm definition
ax = a , so it is possible only if x = 1
Therefore ax = a 1 ⇔ x = 1.
Hence log a a = 1 for all a > 0 , a ≠ 1
Please go through the below link for logarithm formula sheet
Logarithm Tutorial | Exercise – 2
Please go through the below link for logarithm applications with examples and solutions
Logarithm Tutorial | Exercise – 3
Related Articles
Lines | Line segments | Rays | All Math Tricks
Factoring Polynomials by using Basic Algebraic Expressions
Factor Theorem Applications| Factor theorem example problems
Algebra division| Dividing Polynomials Long Division


