In this article explained about some basic concepts in geometry like definitions of lines, line segment and ray. Also explained properties and differences for the same.
Lines | Line segments | Rays | All Math Tricks
Line
A line is breadthless length. Line is a set of infinite points which extend indefinitely in both directions without width or thickness.
A line can be defined as the shortest distance between any two points.
From the above figure line has only one dimension of length.
A line may be straight line or curved line. But generally the word “line” usually refers to a straight line.
Properties of Lines:
1 . Line is the shortest distance path between two points extending indefinitely in both the directions
2. The length of the line not defined
3. A line has no end points and has infinite number of points on it.
4. We are unable to draw a line on a paper just we represent it on paper.
5. A line denoted by ” ” . Here the arrow heads in opposite directions of line suggests that it extends in definitely in both the directions.
6. We also denoted by small English alphabets as l, m, n . . . . etc ( ,
,
, . . . . etc)
Generally the basic idea of a line is its straightness
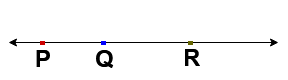Line PQ , Line QR, Line PR , Line PQ , Line QR, Line RP . . . . . . . etc , ( ,
,
. . . . . . . etc )
Line AB , Line AC, Line AD, Line BC , Line CD, Line CB, . . . . . . . . etc ( ,
,
, . . . . . . etc )
Line-segment
A line-segment is a part or portion of a line with two end points. It is the set of all points between the end points and also including endpoints.
For example P and Q be two points in a plane and “l” be the line passing through P and Q. The portion of the line “l” between points P and Q is called the line segment PQ. It is denoted by
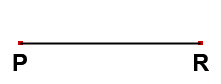
In the above figure P and Q are two points and the shortest distance between them is called a line segment.
Line segments in the above figure – AB, AC, AD, BC, BD & CD
So total line segments – 6 nos.
Properties of line segment
1. Line segment is a path between two points
2. It is named using its two end points
3. Line segment has definite length
4. The distance between two points P and Q is called length of denoted as PQ.
Congruent line segments:
Two lines segments are said to be congruent, if their lengths are equal.
Ray
A ray can be defined as, it is a part of a line with one end point. A line segment extending endlessly in one direction is called Ray.
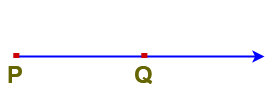
Here PQ is a ray with initial point P and it is denoted as ” “
Properties of Ray:
1. A ray has only one endpoint also called initial point or starting point.
2. A ray has no definite length.
3. There is one and only one ray having given point as initial point and passing through another given point.
In the above figure is one and only one ray having initial point P and passing through another point Q
4. In the below figure is a ray with starting point P and
is a ray with starting point Q. Here
and
are different.
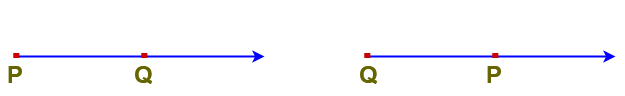
5. Infinite number of rays can be drawn with the the same initial point.
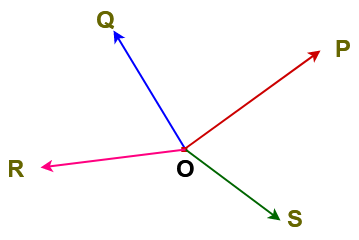
Here ,
,
,
are rays with same initial point O.
6. Since a ray is endless in one direction. We are unable to draw it on paper but just we represent it.
Opposite Rays: Two rays with same initial point and extending indefinitely in opposite directions along the same line, then such rays are called opposite rays.
Here ,
are called opposite rays.
Related Topics:
Point in Geometry | Collinear Points and non-collinear points Examples
Types of Triangles With examples | Properties of Triangle
Quadrilateral Properties | Trapezium, parallelogram, Rhombus
Two dimensional shapes formulas.
Properties of circle in math | Arc, Perimeter, Segment of circle
Thanks for reading. I Hope you liked this article “Definitions and Properties of Line, Line segment and Ray in math”. Give feed back, comments and please don’t forget to share it.
