Two dimensional shapes formulas of area and perimeter calculation

Formulas for two dimensional | Triangle, Quadrilateral, Circle

What is two dimensional shape

A shape with only having two dimensions of width and height and not having another dimension like thickness then it is called two dimensional shape. For example  Circles, Triangles, rectangle, Squares, … etc are called two dimensional objects.

Two dimensional shape also known as “2D”.

In this article cover maximum all two dimensional shapes propertied with formulas of area and perimeter calculations.

Formulas of a Triangle:

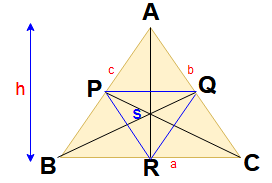
Area of the triangle = (1/2) x Base x Height

Area of the triangle ABC = (1/2) x  a x h

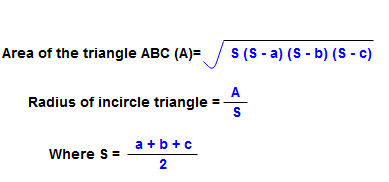
For more concepts regarding the triangles please go through the below link

Classification according to angle and according to sides like Equilateral, isosceles, Scalene, acute angled triangle, Right angled triangle and obtuse angled triangle etc.  | Properties of the Triangles

 

Trapezium (Trapezoid) :

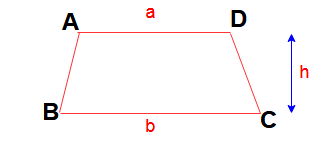
Here AD || BC ,  Height from base AD to base BC is ” h”  and length of AD = a and BC = b

Then Area of  Trapezium (Trapezoid)  ABCD = (1/2 ) (a + b) h.

 

 

Parallelogram:

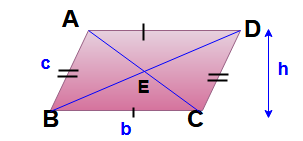
Area of  parallelogram =  bh

Perimeter of  parallelogram = 2 ( b+ h)

 

 

Rectangle:

 

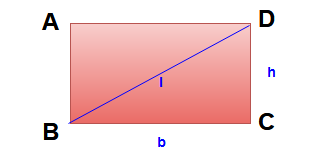
Area of the rectangle = bh

Perimeter of the rectangle = 2 (b + h)

Length of diagonal  ( l )   = √ b² + h²

 

Rhombus:

 

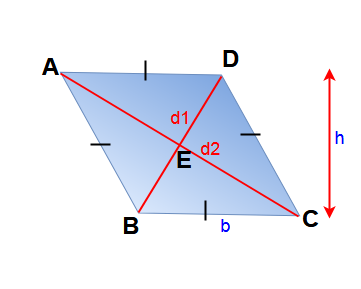
Here $h=$ height,   AB = BC = CD = DA = b & AB || DC , AD || BC

$d1,d2$ are the diagonals

Area of the Rhombus ABCD = bh

Area of the Rhombus ABCD = (1/2) d1 d2

Perimeter of rhombus = 4b

 

 

Square :

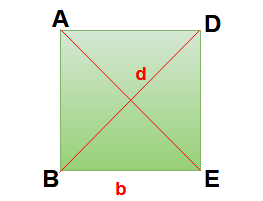
Here length of the side for square ABCD = a

Length of diagonal = d = √2  a

Area of the square = b²

Area of the square ABCD = (1/2) d²

Perimeter of the square = 4b

 

Kite:

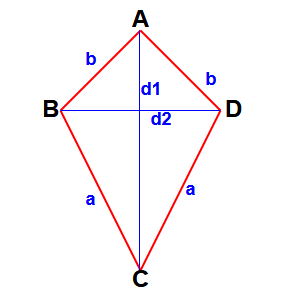
Here BC = DC = a & AB = AD = b

d1 is the length of a diagonal.

d2 is the length of the other diagonal.

Area of kite = (1/2) d1 d2.

 

 

 

 

For more concepts regarding the Quadrilateral please go through the below link

Types of Quadrilateral | Quadrilateral Properties

Area and circumference of a circle:

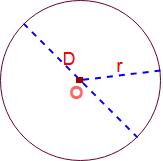Here Origin of the circle = O , Diameter = D and Radius = r

Area of a circle (A ) = π r ² =( π/4 ) D² = 0.7854 D²
Circumference of a circle ( C ) = 2 π r = π D.

Area of circle =( 1/2) x Circumference x radius

A = (1/2) x C x  r

Diameter of a circle (D) = √(A/0.7854).

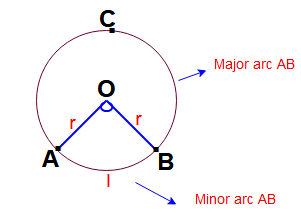
Arc and sector of a circle:

Here angle between two radii is ” θ” in degrees. . And sector of a circle AOB.
Arc length  of circle( l ) (minor) =  ( θ /360) x 2 π r = θ π r / 180

Area of the sector (minor) = ( θ /360) x π r ²

If the angle θ is in radians, then

The area of the sector = (θ/2) r ²

Sector angle of a circle θ = (180 x  l )/ (π r ).

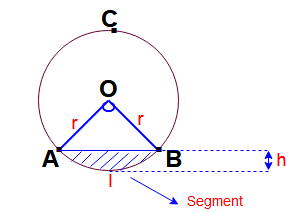
Segment of circle and perimeter of segment:

Here radius of circle = r , angle between two radii is ” θ” in degrees.

Area of the segment of circle = Area of the sector – Area of ΔOAB.

Area of the segment = ( θ /360) x π r ²  +  ( 1 /2) x  sinθ  x r ²

Perimeter of the segment = (θ π r / 180) + 2r sin (θ/2).

Chord length of the circle =  2  √ [ h (2r – h ) ]

Arc  Length of the circle segment   =  l  = 0.01745 x r x θ

Online calculator for circle segment area calculation

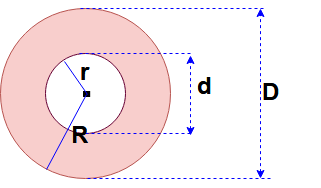
Area of the circular ring:

Here big circle radius = R and Dia = D,

Small circle radius = r and Dia = d,

Area of a circular ring  = 0.7854 (D ² – d ²) = (π/4)  ( D ² – d ²)

Area of a circular ring  = π (R ² – r ² ).

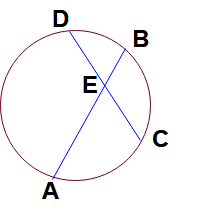
Formula for intersecting chords in circle:

Here AB and CD are two chords in circle and intersecting each at the point E.

Then AE : EB = DE : EC.

 

 

 

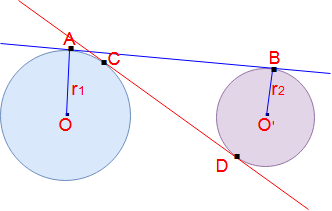
Formula for length of the tangents of circles:

Here Two circles origins O & O’  and radius are r1 and r2 respectively.

Direct common tangent  AB &  transverse common tangent = CD

Length of  direct common tangent AB = √ [ (Distance between two origins)² – (r1 -r2)² ]

= √ [ (OO’)² – (r1 -r2)² ]

Length of transverse common tangent AB = √ [ (Distance between two origins)² – (r1 +r2)² ]

= √ [ (OO’)² – (r1 +r2)² ]

For more concepts regarding the circles please go through the below link

Properties of  circle in math |  Arc, Perimeter, Segment of circle

Area and perimeter of an Ellipse :

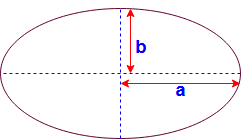
Here Major axis length $=2\mathrm{a\; \&}$Minor axis length $=2\mathrm{b,\; Then.}$

Area of an Ellipse $=\pi a\mathrm{b.}$

Perimeter of an Ellipse = $\mathrm{\pi (}\mathrm{a\; +}\mathrm{b)}$

 

Math Geometry :

Properties of  circle in math |  Arc, Perimeter, Segment of circle

Quadrilateral Properties | Trapezium, parallelogram, Rhombus

Types of Triangles With examples | Properties of  Triangle

Hi friends Thanks for reading. I Hope you liked it. Give feed back, comments and please don’t forget to share it.