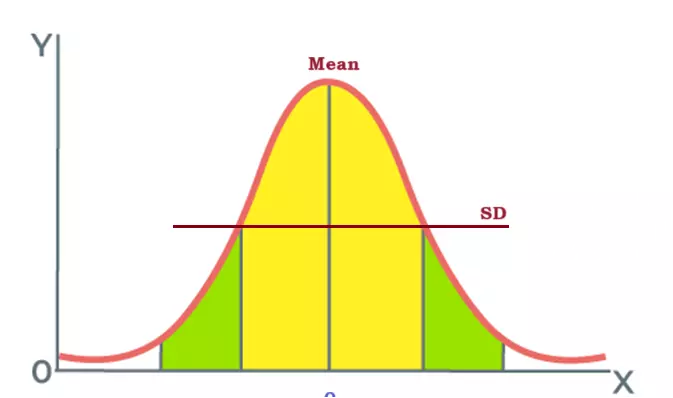
Introduction: Standard deviation is like a measure of how spread out a group of numbers is. It helps us understand if the numbers are close together or scattered far apart. For example, Imagine you have a bunch of test scores the standard deviation helps you figure out if most students scored close to the average or if there are some who did way better or worse.
In various fields, standard deviation aids in risk assessment, quality control, finance, and understanding patterns in scientific research.
The following terms are required to know before going to learn about standard deviation.
Dataset: A dataset is just a collection of numbers that go together. It’s the group of numbers you want to study. If you’re looking at the test scores of a whole class, that’s your dataset.
Mean (Average): The mean is just the average of a set of numbers. You add up all the numbers and divide by how many there are. If you have the scores 70, 80, and 90, the mean is (70 + 80 + 90) ÷ 3 = 80. It’s like the middle point.
Variance: Variance shows how much each number in a group differs from the average. It’s a way of measuring how spread out the numbers are. In the above example if most of the test scores are close to 80, the variance is low. If some are 50 and others are 100, the variance is high.
Dispersion: Dispersion means how spread out the numbers are. If they’re all close to the average, there’s low dispersion. If they’re all over the place, there’s high dispersion. If the test scores are all very similar, there’s low dispersion. If they vary a lot, there’s high dispersion.
Coefficient of Variation (CV): Coefficient of Variation tells us how much variation there is compared to the average. It helps us understand if the numbers are relatively consistent or all over the place. If the test scores have low CV, it means they are pretty consistent. If the CV is high, scores are more varied.
Standard deviation definition with explanation:
Standard deviation is the spread of dataset values around the mean value. The mean is a middle value of all dataset values. It is the spread of all statistical data around a mean value. The graphical representation of standard deviation assists you in understanding the spread of all dataset values.
A low value calculated by the Standard Deviation indicates all data is tightly packed. In this condition, all statistical data is closely near to the data set value. On the other hand, if data values are well spread around the mean value. The standard deviation values are always on the higher side.
Standard deviation is a key concept in analyzing the nature of a sample. You can access population demographics with the assistance of standard deviation. Standard deviation is a degree of measure about the dispersion of data values.
Being a statistician it is necessary to know that a low standard deviation indicates that all data is clustered around the mean. On the other hand, if the standard deviation value is high, then a high standard deviation indicates is spread out around the mean value.
Standard Deviation Symbol:
The symbol used to represent standard deviation is “σ” (sigma) or “s” . When you see this symbol in the context of statistics, it indicates the measure of dispersion in a dataset.
Standard Deviation Formula:
The standard deviation is calculated using a step-by-step process. The formula involves finding the mean, calculating the differences between each data point and the mean, squaring those differences, summing them up, dividing by the number of data points, and finally, taking the square root.
There are two formulas for standard deviation, each serving a distinct purpose: one for calculating the standard deviation of sample data and the other for determining the standard deviation of a given population.
Population Standard Deviation (σ) :
Since we have the entire population, we use N in the denominator. The mean μ is calculated using the entire population.
Mathematically, it is represented as:
\[ \sigma = \sqrt{\frac{\sum_{i=1}^{N}(X_i – \mu )^2}{N}} \]
\begin{align*} & \sigma && \text{represents the standard deviation} \\ & \sum_{i=1}^{N} && \text{denotes the summation over all data points from 1 to N} \\ & X_i && \text{denotes each individual data point} \\ & (\mu) && \text{is the symbol for the is the population mean} \\ & N && \text{is the symbol for the total number of data points in the population} \end{align*}
Sample Standard Deviation (s):
In a sample, we use n−1 in the denominator. This correction, known as Bessel’s correction, accounts for the fact that when we calculate the sample mean, we’re using the sample itself, which introduces a slight bias. Using n−1 instead of n corrects for this bias and provides a more accurate estimate of the population standard deviation.
\[ s = \sqrt{\frac{\sum_{i=1}^{n}(X_i – \bar{X})^2}{n-1}} \]
\begin{align*} & s && \text{represents the standard deviation} \\ & \sum_{i=1}^{n} && \text{denotes the summation over all data points from 1 to n} \\ & X_i && \text{denotes each individual data point} \\ & (\bar{X}) && \text{is the symbol for the sample mean} \\ & n && \text{is the symbol for the total number of data points in the sample} \end{align*}
The applications of both population standard deviation (σ) and sample standard deviation (s)
Population Standard Deviation (σ): It will be used when you have data for the entire group or population. It helps in understanding how spread out all the data points are in the entire group. If you have information about everyone or everything you’re interested in (the entire group), use (σ)
Sample Standard Deviation (s): It will be used when you only have a smaller group or subset of the entire population. It’s used when you want to estimate the spread of the entire population based on a smaller sample. The n−1 correction helps to make the estimate more accurate.
If you only have information about a smaller group or subset, use “s” and make sure to use the n−1 correction for a more accurate estimate.
For example , Imagine you want to know the average height of all students in a school (population). You’d use σ. If you only measured the height of a few students (sample), you’d use s, and the n−1 correction helps adjust for the fact that you’re working with a smaller group.
In essence, σ is for the big picture when you have everything, and s is for when you’re working with a smaller part and want to make good estimates about the whole.
Standard Deviation vs Variance:
While standard deviation measures the absolute dispersion of data, variance is its squared counterpart. Variance is calculated by averaging the squared differences between each data point and the mean. Essentially, the standard deviation is the square root of the variance. Comparatively, standard deviation is often preferred as it is in the same units as the original data, making it more interpretable.
Standard Deviation vs Coefficient of Variation:
The Coefficient of Variation (CV) is another statistical measure, but unlike standard deviation, it expresses the relative variability of a dataset. CV is calculated by dividing the standard deviation by the mean and multiplying by 100 to express it as a percentage. While standard deviation gives us the absolute measure of variability, the coefficient of variation offers a relative measure, making it easier to compare the consistency of datasets with different means.
\[ \ CV = \left( \frac{\sigma}{\bar{x}} \right) \times 100 \]
Standard Deviation Calculation Example:
Example -1: Consider a dataset: 5, 7, 3, 7 . Find the sample standard deviation
Step 1: Find Mean (x̄ )
Add all values = 5+7+3+ 7 = 22
Mean
Calculate Variance for each term:
Calculate Variance:
Sum of Square of Variance of all terms = (0.25 + 2.25 + 6.25 + 0.25) = 11
Variance of all terms = 11/ (N-1)
Variance of all terms = 11/ (4-1) =
Find Standard Deviation (s):
Example 2: Let’s consider the following statistical data 4,9,6,9,10,4,5,12,4,7,3,9,11,8,7,12,4,5,2,9. Find the population standard deviation
There is a sequence of procedures in the standards deviation first need to find the mean values. Then you are going to subtract these mean values from the dataset values.
Step 1: Find Mean
Add all data set values to find the mean.
4+9+6+9+10+4+5+12+4+7+3+9+11+8+7+12+4+5+2+9 = 140
The sum of all values = 140
Number of dataset values = 20
Mean = μ =Total Number/N = 140/20 = 7
The standard deviation calculator calculates mean values.
Step 2: Find a Square
Now subtract all the values from the mean and find the square of all dataset values.
(4 – 7)2 = (-3)2 = 9
(9 – 7)2 = (2)2 = 4
(6 – 7)2 = (-1)2 = 1
(9 – 7)2 = (2)2 = 4
(10 – 7)2 = (3)2 = 9
(4 – 7)2 = (-3)2 = 9
(5 – 7)2 = (-2)2 = 4
(12 – 7)2 = (5)2 = 25
(4 – 7)2 = (-3)2 = 9
(7 – 7)2 = (0)2 = 0
(3 – 7)2 = (-4)2 = 16
(9 – 7)2 = (2)2 = 4
(11 – 7)2 = (4)2 = 16
(7 – 7)2 = (0)2 = 0
(8 – 7)2 = (1)2 = 1
(12 – 7)2 = (5)2 = 25
(4 – 7)2 = (-3)2 = 9
(5 – 7)2 = (-2)2 = 4
(2 – 7)2 = (-5)2 = 25
(9 – 7)2 = (2)2 = 4
The squares of all values are then used to find variance.
Step 3: Find Variance
The sum of all square values = 178
Now Sum number of N = 20
Variance = σ 2 = 178/ N = 178/ 20 = 8.9
Step 4: Find a Standard Deviation
Take the square root of the variance to find the standard deviation.
Standard deviation = σ = √(8.9) = 2.983
Online Calculator for Standard Deviation
SD calculator online has a tool for finding variance and standard deviation of given statistical data.
Answering Common Questions:
Q1: What does a low standard deviation mean? A low standard deviation indicates that the data points are closely packed around the mean, signifying a more consistent dataset.
Q2: What does a high standard deviation mean? Conversely, a high standard deviation suggests that the data points are scattered more widely, indicating greater variability in the dataset.
Q3: How does standard deviation help in data analysis? Standard deviation helps analysts understand the degree of variability or dispersion in a dataset, providing insights into the data’s nature and distribution.
Q4: Can standard deviation be negative? No, standard deviation cannot be negative. It is a measure of dispersion and is always a non-negative value.
Q5: Can standard deviation be zero? Yes, if all data points in a dataset are identical, the standard deviation is zero, indicating no variability.
Related Articles:
Centroid of the triangle meaning, definition, properties, formula with examples and calculator
Frustum of cone formulas with examples | Surface area and Volume
Surface Area and Volume of a Prism Formulas, rectangular and triangular
Relationship Between Arithmetic, Geometric, Harmonic Mean. AM, GM and HM
Harmonic Progression and Harmonic Mean formulas with properties
Geometric Sequences Practice Problems | Geometric Progression Tutorial
Basic Concept, formula with examples for Arithmetic Mean
Arithmetic Progression Problems with Answers for Competitive Exams