Surface Area and Volume of a Prism Formulas, rectangular and triangular

Formulas of a Prism – Surface Area and Volume

What is Prism

A prism mathematically defined as, It is a solid three dimensional object which can have any polygon at both its ends.

Prism can be also defined as a polyhedron with two polygonal bases parallel to each other

The prism two faces is called the ends and other faces are called the lateral faces or side faces. Its dimensions are defined by dimensions of the polygon at its ends and its height. The lateral faces are mostly rectangular.

The prism is mostly used in physics. According to this view a prism is defined as the transparent optical element with polished into geometrical and optically significant shapes of lateral faces join the two polygonal bases. The flat polished surfaces are refract light.

Right Prism & Oblique Prism

The side-edges of a right prism are perpendicular to its base or ends. If the side-edges of a prism are not perpendicular to its ends then it is called as an Oblique prism.

Lateral surface area of the right prism = Perimeter of base (P) x height (h)

Total surface area of the right prism = Lateral surface area of the right prism + The area of the two plane ends

Volume of right prism = Area of the base ( B) x height ( h)

Prism can be classified into different types according to their base shape.

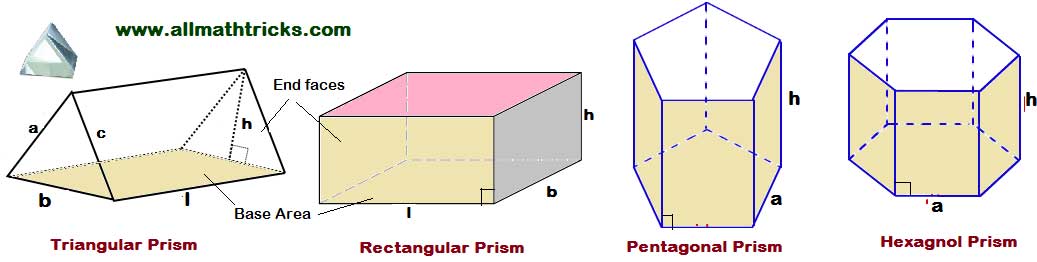
Triangular Prism

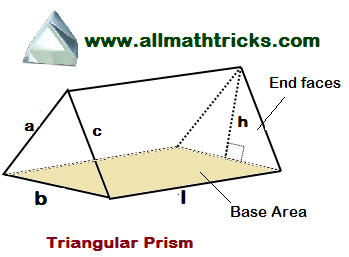
Rectangular Prism

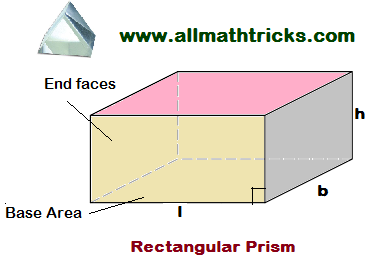
Pentagonal Prism

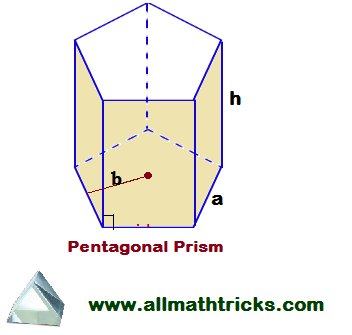
Hexagonal Prism

Octagonal prism

Polygonal prism

A prism is said to be triangular if its two ends are triangles; it is called rectangular if its ends are rectangles; and so on. i.e A prism is said to be polygonal if its two ends are polygons

Here we are discussing about prism formulas for right prim

Triangular Prism formulas

A Prism having two parallel triangular surfaces, one rectangular base and two rectangular surfaces are inclined to each other then is is called triangular prism.

Lateral surface area of the triangular prism = Perimeter of triangle x l = (a + b + c) l

Total surface area of a triangular prism formula = (2 × Triangular Base Area) + (Triangular Base Perimeter × Length) = (Apothem length x base length) + 3 (base length x height)

Total Surface area of triangular prism = 2B + Pl = (2 x Triangle area) + [ ( a + b + c ) l ]

Triangle area = B $= \frac{1}{2} \times b \ h$ = $\sqrt{s(s-a)(s-b)(s-b)}$

(Apothem length = h/2)

Where $S = \frac{a+b+c}{2}$ ( According to heron’s formula)

The volume of a triangular prism = Area of base triangular prism × height

Volume of triangular prism = B x l = $\frac{1}{2} \times \ lbh$

Here B = Base area of the prism

l = Base length of a prism

b = base width of a prism

h = height of the prism

a & c = sides of the triangular base

Rectangular Prism Formulas

A Prism having two rectangular bases are parallel to each other and its ends are joining with four rectangular faces then it is called as a rectangular prism.

Total surface area of a rectangular prism = (base width x height) + (height x base length) + 2 x (base length x base width)

Lateral surface area of the Rectangular Prism = Ph = 2h ( l + b)

Total Surface area of Rectangular Prism = 2B + Ph = 2 ( lb + bh + hl)

Volume of a rectangular prism = Base area x height = base width x base length x height

Volume of Rectangular Prism = Bh = lbh

Pentagonal Prism Formulas

A Prism having two pentagonal base surfaces are parallel to each other and five rectangular surfaces are inclined to each other then it is called pentagonal prism.

a = Base or side length of pentagonal prism
b = Apothem length
h= Height of pentagonal prism

Formula of pentagonal prism surface area = 5 x (apothem length x base length) + 5 x (base length x height)

Surface Area of pentagonal prism = (5ab + 5ah)

The volume of a pentagonal prism formula $= \frac{5}{2} \times \ apothem \ length \times \ base \ length \times \ height$

Volume of pentagonal prism = $\frac{5}{2} \times \ abh$

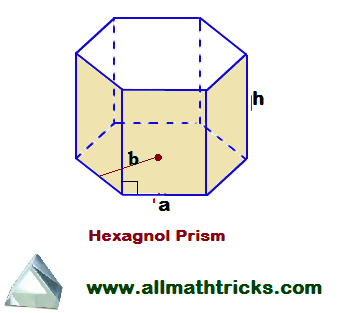
Hexagonal Prism Formulas

A Prism having two hexagonal base surfaces are parallel to each other and six rectangular surfaces are inclined to each other then it is called Hexagonal prism.

Here

a = Base or side length of hexgon prism
b = Apothem length
h= Height of prism

The total surface area of a hexagonal prism formula = 2 (area of hexagon base ) + 6 ( Area of rectangle face)

= 6 x (base length x apothem length ) + 6 x (base length x height)

= 2 ( 3ab) + 6ah = 6a ( b + h)

Surface area of the hexagonal prism $= \ 3 \sqrt{3} \ a^2 \ + 6 \ a \ h$

Volume of the hexagonal prism = 3 x base length x apothem length x height = 3 abh

Volume of the hexagonal prism $= \ \frac{3}{2} \times \ \sqrt{3} \ a^2 \ h$

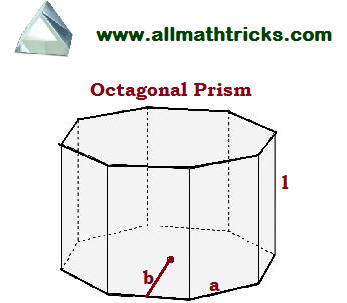
Octagonal prism

A Prism having two octagonal base surfaces are parallel to each other and ten rectangular surfaces are inclined to each other then it is called Octagonal prism. This prism having a total of 24 edges , 10 faces and 16 vertices.