Volume of cube and cuboid, Area of cube and cuboid

In this page provided formulas for Surface Area, volume, Diagonal Length, Perimeter of Cuboid and Cube with examples

Surface Area and volume of cuboid and Cube Formulas with Examples

Cuboid

A solid which contains length, breadth and height is called cuboid. A cuboid is three dimensional box. It is virtue of its length (l), breadth ( b) and height (h).

Cube

A cube is a cuboid which has all its edges equal

i,e length = breadth = height = a

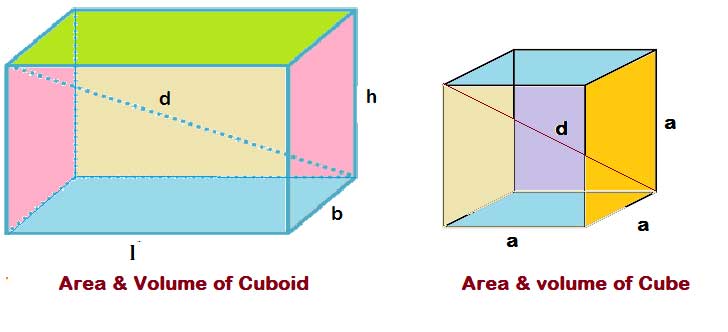
A cuboid or cube have 6 faces, 8 vertices and 12 edges.

Perimeter of Cuboid and Cube

The perimeter of the cube or cuboid gives the complete edge to edge separation of the shape of the same

Perimeter of Cuboid = 4 ( l + b + h)

Perimeter of cube = 4 ( a + a + a ) = 12a

Surface Area of Cuboid and Cube

The area of four faces of cube or cuboid is called the lateral surface area of the same.

Lateral Surface area of cuboid = lh + lh + bh + bh = 2 (lh + bh) = 2 (l +b)h

Lateral Surface area of cube = aa + aa + aa + aa = 4a²

Six rectangular pieces are covered by cuboid total surface area.

Total surface area of cuboid = Total area of the all rectangular pieces = lb + lb + bh + bh + lh + lh

Area of Cuboid = 2 ( lb + bh + lh)

Total surface area of cube = Total area of the all square pieces = aa + aa + aa + aa+ aa + aa

Area of Cube = 6a²

Volume of Cuboid and Cube

Cuboid or cube measure of this occupied space is called the volume of Cuboid and Cube.

The total surface area of cuboid = The area of plan rectangle occupied by each rectangle x height = Length x Breadth x Height

Volume of the Cuboid =( l x b x h) cubic units

Volume of Cube = edge x edge x edge = a x a x a = a³cubic units

Diagonal length of Cuboid and Cube

Diagonal a Cuboid (d) = $\sqrt{l^2 +b^2 +h^2}$

Diagonal a Cube (d) = $\sqrt{3a}$

Formulas of Cuboid and Cube

Description	Cuboid	Cube
Perimeter	4 ( l + b + h)	12a
Lateral Surface area	2 (l +b)h	4a²
Total surface area	2 ( lb + bh + lh)	6a²
Volume	( l x b x h)	a³
Diagonal Length	$\sqrt{l^2 +b^2 +h^2}$	$\sqrt{3a}$

Examples of Cuboid and Cube

Ex – 1 : The required rectangular box has length, breadth and height as 80 cm, 40 cm and 20 cm respectively. Then how many Square sheets are required to prepare rectangular box with side of 40 cm.

Solution: Here rectangular box

Length = l = 80 cm ,

Breadth = b = 40 cm &

Height = h = 20 cm

Side of the square sheet = a = 40 cm

Total surface area of the rectangular box = 2 (lb + bh + lh ) = 2 [ (80 x 40) + (40 x 20) + (80 x 20)] = 11200 cm²

The surface area one single square sheet = 2 a² = 2 x 40 x 40 =1600 cm²

Therefore, number of square sheets required for prepare a rectangular box = Total surface area of the rectangular box / Total surface area of the rectangular box

= 11200 / 1600 = 7

Hence 7 sheets are required.

Ex-2 : The length of a rice godown is double its breadth. Its height is 3 m. The area of four walls is 108 m². Find the volume of the godown.

Solution: Take godown breadth = b m then length = l = 2b m, height = 3 m

Area of four sides = 2(l+b)h = 108

⇒ 2 ( 2b + b) 3 = 108

⇒ b = 6 m

⇒ l = 2b = 12 m

Volume of rice godown = 12 x 6 x 3 = 216 m³

Ex-3 : A solid cube of lead having edge measures 44 cm. How many spherical balls can be made by using solid cube of lead and each ball being 88 cm in diameter.

Solution:

Side of the solid cube lead = a = 44 cm

Volume of the solid cube = a³ = 44³

Radius of spherical balls = r = 88/2 = 44 cm

Volume of each spherical ball = $\frac{4}{3} \pi \ r^3$ = ( 4/3) x (22/7) x (3 x 3 x 3 )