In this article, we will get an idea of the initial understanding of Coordinate geometry concepts like the cartesian plane, quadrants, X-coordinate (abscissa), Y-coordinate (ordinate), and how to plot the points on a coordinate plane.
Basic Concepts of Coordinate Geometry
Coordinate geometry is one of the important concept in mathematics. Coordinate Geometry is one of the new branch of mathematics to representation of a point on a plane with idea of two references.
The concepts of Co-ordinate Geometry were developed by Rene Descartes (1596-1650). He is a French mathematician and philosopher and he is established an association between algebraic equations and geometric curves and figures.
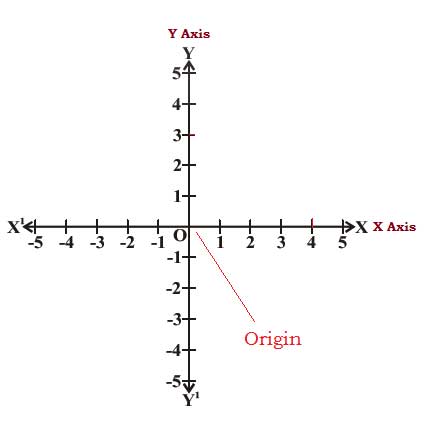
In the above figure we draw a vertical number line and horizontal number line meeting at a point perpendicular to each other. The intersection point is denoted as origin.
The horizontal number line XX1 is known as X-axis, and the vertical number line YY1 is known as the Y-axis.
The point where XX1 & YY1 intersect each other is called the origin, and is denoted by ‘O’.
In this plane the positive numbers lie on the directions OX is called the positive direction of the X-axis, similarly OY is the positive Y-axis respectively. Also the negative numbers lie on the directions OX1 is called the negative directions of the X-axis, similarly OY 1 is the negative Y-axis respectively.
The plane here is known as the cartesian plane or co-ordinate plane or XY-plane. The X & Y axes are known as coordinate axes.
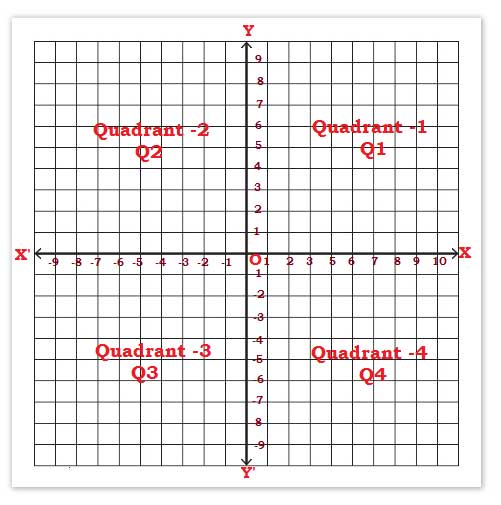
The coordinate plane is divided into four parts by these coordinate axes. These four parts are called the quadrants and are denoted by Quadrant -1 (Q1), Quadrant -2(Q2), Quadrant -3(Q3) & Quadrant -4( Q4) in anti clockwise direction.
Coordinates of a Point ( or) Locating coordinate points
A quadrant is also defined as a part of a Cartesian or coordinate plane obtained when the two axes intersect each other.
Quadrant -1 (Q1) : x > 0, y > 0 (+x, +y)
Quadrant -2 (Q2) : x < 0, y > 0 (- x, +y)
Quadrant -3 (Q3) : x < 0, y < 0 (-x, -y)
Quadrant -4 (Q4) : x > 0, y < 0 (+x, – y)
X coordinate – The X-coordinate of a point is the distance from the origin to the foot of the perpendicular on X-axis. The x-coordinate is also known as the abscissa.
Y coordinate – The Y-coordinate of a point is the distance from the origin to the foot of the perpendicular on the Y-axis. The y-coordinate is also known as the ordinate.
In the coordinate system, the origin as a reference point to locate other points in a plane.
A coordinate states the location of a point in two-dimensional space. The coordinates of a point are shown as (x, y).
Coordinates of Origin: The point “O” lies on the Y-axis. Its distance from the Y-axis is zero. Hence, its x-coordinate is
zero. Also, it lies onthe X-axis. Its distance from the X-axis is zero. Hence, its y-coordinate is zero.
So the coordinates of the origin “O” are denoted as a (0,0).
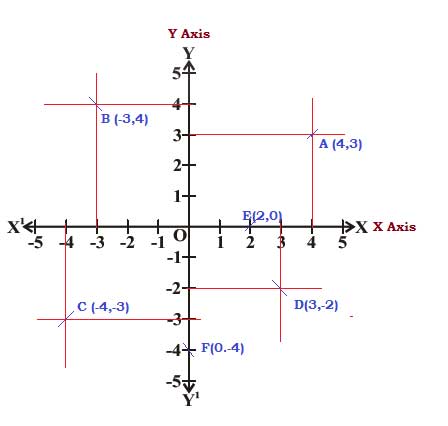
The point “A” is at a distance of 4 units from the Y-axis measured along a positive point of the X-axis from the origin. The same point is at a distance of 3 units from X-axis, measured along a positive point of Y-axis from the origin.
The x-coordinate (abscissa) of A is 4, & The y-coordinate (ordinate) of A is 3.
Hence, the coordinates of A are (4,3)
The x-coordinate (abscissa) of B is -3 & The y-coordinate (ordinate) of B is 4.
Hence, the coordinates of B are (-3,4)
The x-coordinate (abscissa) of C is -3 & The y-coordinate (ordinate) of C is -4.
Hence, the coordinates of C are (-3,-4)
The x-coordinate (abscissa) of D is 3 & The y-coordinate (ordinate) of D is -2.
Hence, the coordinates of D are (3, -2)
The point “E” is at a distance of +2 units from the Y-axis and at a distance zero from the X-axis. Therefore the x-coordinate of “E” is 2 and the y-coordinate is 0.
Hence, the coordinates of “E” are (2,0).
The point “F” is at a distance of -4 units from the X-axis and at a distance zero from the Y-axis. Therefore the x-coordinate of “F” is 0 and the y-coordinate is -4.
Hence, the coordinates of “F” are (0, -4)
Summary of Coordinates Geometry Introduction
1) The concepts of Coordinate Geometry were developed by Rene Descartes (1596-1650).
2) The plane in coordinate geometry is known as the cartesian plane or co-ordinate plane or XY-plane.
3) The axes are called the coordinate axes. The axes are called the coordinate axes.
4) The intersection point of the x and the y-axis is denoted as origin. At this point of origin, both values x & y-coordinates are zero.
5) The coordinate axes divide the plane into four parts. These four parts are known as the quadrants
6) The point has to be located on the plane by a set of two numbers of (x,y)
7) Y- coordinate is known as the ordinate & X – X-coordinate is known as the abscissa
Related articles:
Point in Geometry Math | Collinear Points and non-collinear points Examples
Lines in Geometry | line segment math definition | Ray along with their types
Types of Lines | Straight and Curved Line | Lines In Geometry
Transversal Angles | Angles formed by parallel lines and transversal Line
Angles in Math | Acute, Right, Obtuse, Straight, Reflex & Complete angle
Complementary and supplementary angles | Types of Angle Pairs
Types of Triangles with formulas and examples
