Complementary and supplementary angles | Types of Angle Pairs | geometry

In this section we discuss about different types of angles pairs  like Complementary Angles, Supplementary Angles, Conjugate Angles & Congruent angles with examples

Angle Pairs Definition and Examples  | Conjugate and Congruent Angles

For Basic concepts of angles and Different Types of Angles in Geometry like Zero Angle, Acute Angle, Right Angle, Obtuse angle, Straight Angle, Reflex Angle & Complete angle go through the below link

Acute, Right, Obtuse, Straight, Reflex & Complete angle

Complementary Angles

If the sum of two angles are 90^o then the angles are said to be Complementary angles. Each one of these angles is called the Complementary of the other.

Example:

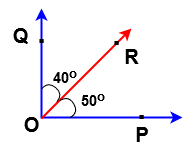
From the above example  ∠POR = 50^o , ∠ROQ = 40^o  are complementary angles

Since sum of the these two angles are 90^o

i.e ∠POR + ∠ROQ  = 50^o + 40^o = 90^o

Here ∠POR is said to be complementary angle of ∠ROQ and ∠ROQ is said to be complementary angle of ∠POR.

How to find complementary angles

If any angle of ‘ y ‘ is less than 90^o then

Complementary angle of  y  = 90^o  – y^o

Supplementary angles

If the sum of two angles are 180^o then the angles are said to be supplementary angles,  . Each one of these angles is called the supplementary of the other.

Example:

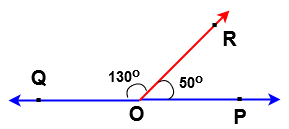
From the above example  ∠POR = 50^o , ∠ROQ = 130^o  are supplementary angles

Since sum of the these two angles are 180^o

i.e ∠POR + ∠ROQ  = 50^o + 130^o = 180^o

Here ∠POR is said to be supplementary angle of ∠ROQ and ∠ROQ is said to be supplementary angle of ∠POR.

How to find supplementary angles

If any angle of Y is less than 180^o then

Supplementary angle of  y  = 180^o  – y^o

Conjugate Angles:

If the sum of two angles are 360 then the angles are said to be Conjugate angles,  . Each one of these angles is called the conjugate of the other.

Example:

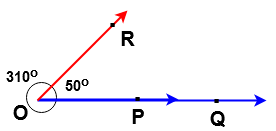
From the above example  ∠POR = 50^o , ∠ROQ = 310^o  are conjugate angles

Since sum of the these two angles are 360^o

i.e ∠POR + ∠ROQ  = 50^o + 310^o = 310^o

Here ∠POR is said to be conjugate angle of ∠ROQ and ∠ROQ is said to be conjugate angle of ∠POR.

How to find conjugate angles

If any angle of  ‘y ‘ is less than 360^o then

Conjugate angle of y  = 360^o  – y^o

Congruent angles:

Two angles having the same measure are known as congruent angle.

In the above figure ∠AOB & ∠POQ  are congruent angles.

Since ∠AOB  =  ∠POQ  = 60^o

Angular bisector:

A ray which divides an angle into two congruent angles is called angular bisector.

Example:

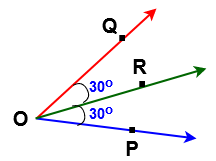
In the above figure ray OR is called angular bisector of ∠POQ.

Since ∠POR = ∠ROQ = 30^o

Thanks for reading this article. I Hope you liked this article “Complementary and supplementary angles meaning with examples”.  Give feed back and comments please.

Related Articles:

Angles are formed by Parallel Lines Cut by a Transversal line

Classifications of Triangles with properties

Quadrilateral with their properties and formulas

Properties of  circle in math  and  Arc, Perimeter, Segment of circle

Lines In Geometry | Types of Lines |  Straight and Curved Line |

Ray along with their types | Line segment math definition

Collinear Points and non-collinear points | Point in Geometry Math