Transversal Angles | Angles formed by parallel lines and transversal Line

In this section we discuss about angles are formed by Parallel Lines Cut by a Transversal line like corresponding angles, Alternate interior lines, Alternate exterior angles , co interior angles and co exterior angles. Also learn about properties of the same angles.

Interior angles  | Exterior Angles | Alternate Interior and Alternate Exterior Angles

What is Transversal Line

The transversal line is defined as ” A line which intersects two or more lines at distinct points”.

For example

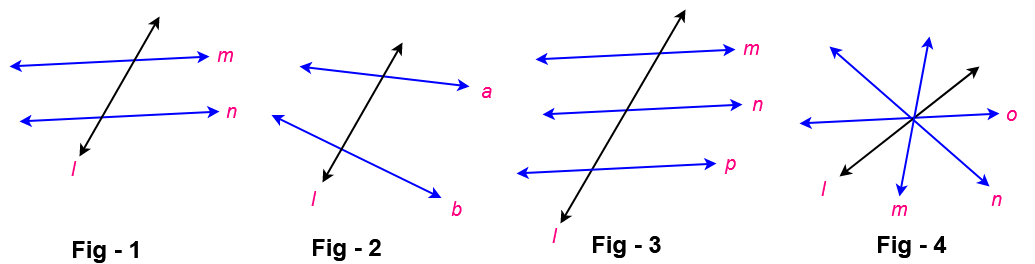
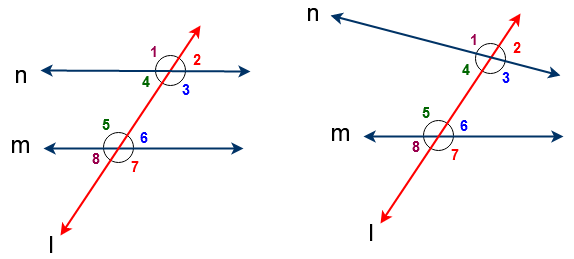
Fig -1 : Here lines ‘ n’ & ‘ m’  are parallel lines and a line  ‘ l’ intersection both lines at distinct points  so a line  ‘ l’ is a transversal to given lines of ‘n’ and ‘ m’

Fig -2 : Here lines ‘ n’ & ‘ m’  are non-parallel lines and a line  ‘ l’ intersection both lines at distinct points  so a line  ‘ l‘ is a transversal to given lines of ‘n’ and ‘ m’

Fig – 4 : Here  line ‘l ‘ is not a transversal

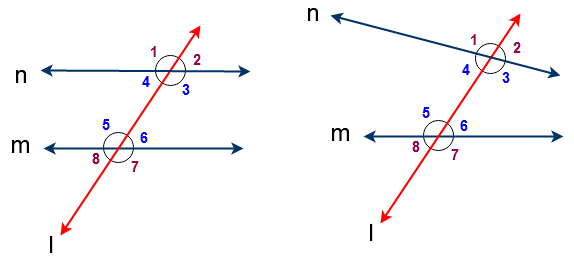
Here ‘ l’ is a transversal for the lines of ‘ m’ and ‘ n‘.

Total eight Angles are formed by parallel lines and transversal Line. Also same eight angles are formed by non-parallel lines and transversal line

So from the above figures angles are formed as follows

∠1 , ∠2 , ∠3 , ∠4 , ∠5 , ∠6 , ∠7 & ∠8

Interior Angles

In the above figure ∠3 , ∠4 , ∠5  & ∠6 are called interior angles since those angles lie in between two lines.

i.e interior of two lines

Exterior Angles

In the above figure ∠1 , ∠2 , ∠7 & ∠8 are called exterior angles since those angles do not lie in between two lines.

i.e outsider of the two lines.

Corresponding angles:

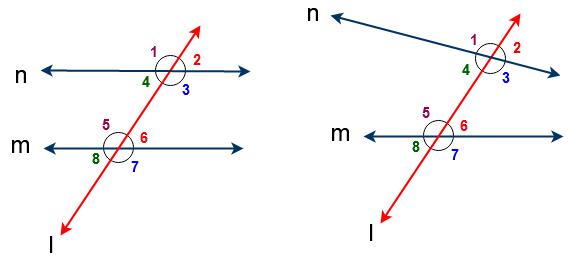
In the above figure ( ∠1 , ∠5 ) , ( ∠2 , ∠6 ) , ( ∠3 , ∠7) , (∠4  ∠8) are the corresponding angles.

i.e Two angles are said to be a pair of corresponding angles if

1. They are on the same side of the transversal

2. One is an interior angles and the other is an exterior angle.

3. They are not adjacent angles.

Alternate interior angles and Alternate exterior angles

Two angles are said to be alternate interior angles if

1. Both are interior angles

2. They are on either side of the transversal

3. They are not adjacent angles

So in the below figure ( ∠4 , ∠6) , ( ∠3 , ∠5 ) are alternate interior angles

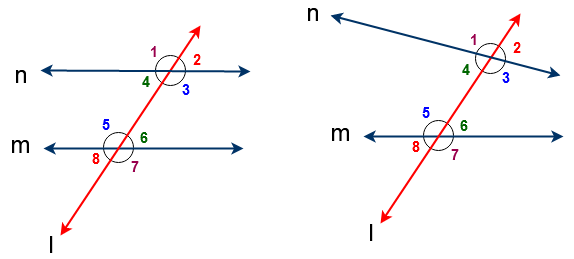
Two angles are said to be alternate exterior angles if

1. Both are exterior angles

2. They are on either side of the transversal

3. They are not adjacent angles

So in the above figure ( ∠1 , ∠7) , ( ∠2, ∠8) are alternate exterior angles

Co-interior angles and Co-exterior angles

Two angles are said to be Co-interior angles if they are interior angles and lies on same side of the transversal. The Co-interior angles also called as consecutive angles or allied interior angles.

So in the below figure ( ∠4, ∠5) , ( ∠3, ∠6) are Co-interior angles or consecutive angles or allied interior angles.

Two angles are said to be Co-exterior angles if they are exterior angles and lies on same side of the transversal.

So in the above figure ( ∠1 ∠8 ) , ( ∠2, ∠7 ) are Co-exterior angles.

Linear Pair of Angles

If the sum of two adjacent angles is 180^o, then they are called a linear pair of angles.

In the below figure ( ∠1 , ∠4 ) , ( ∠1 , ∠2 ) , ( ∠2 , ∠3 ) , ( ∠3 , ∠4 ) , ( ∠5 , ∠6) , ( ∠5 , ∠8), (∠6  ∠7) , & (∠7  ∠8) are linear pair of angles. Hence their sum is 180^o. i.e

∠1  + ∠4  = 180^o    , ∠1  + ∠2  = 180^o , ∠2  + ∠3  = 180^o  , ∠3  + ∠4  = 180^o

& ∠5 + ∠6  = 180^o    , ∠5  + ∠8  = 180^o , ∠6  + ∠7  = 180^o  , ∠7 + ∠8  = 180^o

Vertical Opposite angles

In the above figure ( ∠1 , ∠3 ) , ( ∠2 , ∠4 ) , ( ∠5 , ∠7 ) , ( ∠6 , ∠8 )  are Vertical Opposite angles.

We know that if two lines intersect each other, then the vertically opposite angles are equal. Hence these pairs of angles are equal

∠1  =  ∠3  , ∠2 = ∠4 , ∠5 = ∠7  &  ∠6 = ∠8