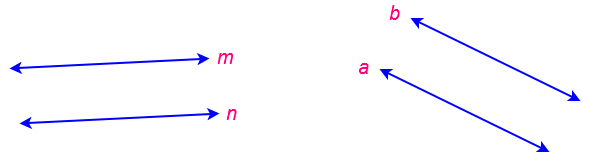In this article explained about different types of lines in geometry like straight line, curved line, Intersecting lines, Concurrent lines, Parallel Lines and transversal line with examples.
Types of Lines | Straight and Curved Line | Lines In Geometry
Definitions and Properties of Line, line segment & ray
Basic concepts in geometry of Line, Line-segment and Ray – Please go through the below link
Types of Lines as per Geometry
1. Straight Line
2. Curved Line
3. Intersecting Lines
4. Concurrent Lines
5. Perpendicular Lines
6. Parallel lines
7. Transversal line
Straight Line
Generally a line refers to a straight line. It is a line which lies evenly with the points on itself.
A line “ l ” is the set of a moving point P, Q and R which moves in such a condition that R is always collinear with the given two fixed points of P & Q then it is called straight line.
Curved Line
The path between two points which has no straightness is called curved line.
Intersecting lines
If two lines in a place have a common point then these lines are said to be intersecting line and their common point is known as Point of intersection.
Example:
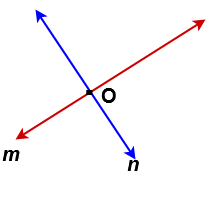
Here m and n are two lines and they are intersecting at a point ” O”. So these lines are called intersecting lines
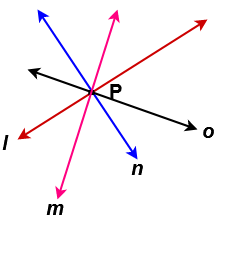
Concurrent lines
If three or more lines passing through the same point they are called concurrent lines and the point through which they pass is called the point of concurrency or concurrent point.
Example:
Here l,m,n & o lines are passing through the same point of ” P ” . So these lines are called Concurrent lines. The point ” P” is called the point of concurrency or concurrent point.
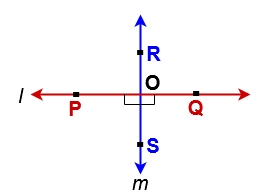
Perpendicular Lines
If the measuring of the angle between two lines is 90o then the two lines are perpendicular lines.
In the above figure l & m are two lines and they are intersection at a point “O“. At a intersecting point four angles ∠POS , ∠QOS , ∠QOR and ∠ROP are formed. Measure these angles. If every angle have right angle i.e 90o then lines l ( ) and m (
) are perpendicular lines.
We write l ⊥ m and read it is “ l “ is perpendicular to “m“
Parallel Lines :
If two lines drawn in a plane such that they don’t intersect, even when extended indefinitely in both the directions, then such lines are called parallel lines.
i.e the lines don’t have intersecting point.
Here Line “n” is parallel to line “m” and we write it as n ∥ m &
Line “a” is parallel to line “b” and we write it as a ∥ b
Properties of parallel lines
1 . The distance between the parallel lines at every where is always same.
2. The angle between two parallel lines is zero.
3. If two lines are parallel to the same line then they are parallel to each other.
Example:
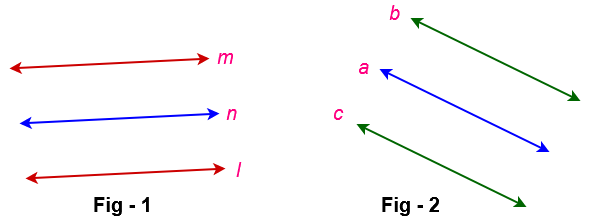
In the figure- 1 , Line ‘ l’ is parallel to line ‘n“ and line ‘n‘ is also parallel to ‘ m‘ . Then line ‘ l’ is parallel to ‘m’.
( i.e l ∥ n & n ∥ m then l ∥ m)
In the figure- 2 , Line ‘ c’ is parallel to line ‘a“and line ‘a‘ is also parallel to ‘ b’ . Then line ‘ c ‘ is parallel to ‘b‘.
( i.e c ∥ a & a ∥ b then c ∥ b )
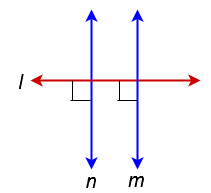
4. If two lines are perpendicular to the same line then they are parallel to each other.
In the above figure line ‘n‘ is perpendicular to ‘ l ‘ and line ‘ m‘ is perpendicular to ‘ l ‘ then ‘m‘ is parallel to ‘n‘.
( i.e n ⊥ l and m ⊥ l then n ∥ m )
Transversal Line
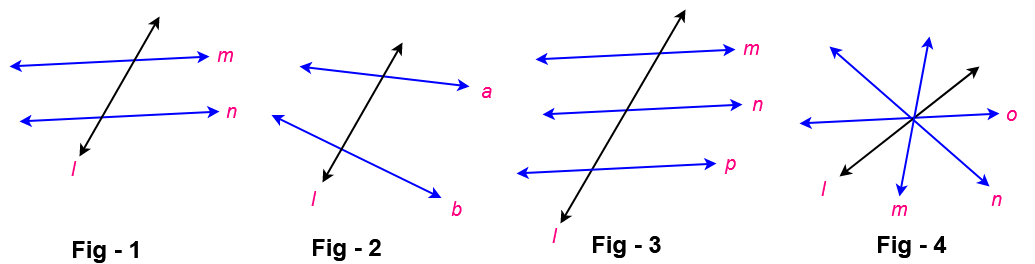
A line which intersecting two or more given lines at different at different points is called a transversal to that lines
Example of Transversal Line
In figure – 1 , 2 and 3 line ‘ l ‘ is a transversal line and in figure – 4 line ‘ l’ is not a transversal line.
Related Topics:
Concepts of Line, Line segment & Ray
Two dimensional shapes formulas.
Point in Geometry | Collinear Points and non-collinear points Examples
Types of Triangles With examples | Properties of Triangle
Quadrilateral Properties | Trapezium, parallelogram, Rhombus
Properties of circle in math | Arc, Perimeter, Segment of circle
Thanks for reading. I Hope you liked this article “different types of lines in geometry”. Give feed back, comments and please don’t forget to share it.