In this article explained about defections of point in geometry math, Collinear Points, Non-collinear points with examples.
Point in Math | Collinear Points | Non-collinear points | All Math Tricks
The terms Point, Line, Plane and space .. etc are fundamental concepts in study of geometry and they
Definition of Point in Math:
A point is that which has no part. It has only one position. It does not have dimensions like length, breadth or height
Consider the step from points to solid
Point – Line – Surface – Solids

In the above figures, the first figure is Point. It has no dimension. If it further add one dimension length then it will be line segment (Line). If further add one more dimension breadth then it will have two dimension which is rectangle(Surface) . Now add one more dimension height then it has three dimension which is cuboid (Solid).
Collinear Points & non-collinear points:
Collinear points : Three or more points lying on the same line are called collinear points.
Non-collinear points : Three or more points are not lying on the same line are called non-collinear points.
Examples
Let us considered three points P, Q and R in a plane. If we draw a line ” l “ passing through two points P & Q , then there are two possibilities
a) Point R lies on the line “ l “
b) Point R does not lie on the line “ l “
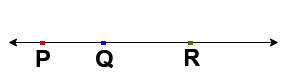
If a point R lies on the line “ l “ then points P , Q & R lie on the same line and are said to be collinear points.
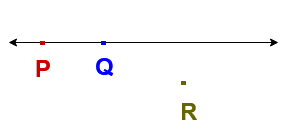
If a point R does not lie on the line “ l “ , then points P, Q and R do not lie on the same line and are said to be non- collinear points.
Lines through non- collinear points
Examples of non-collinear points
Let consider P, Q and R are non- collinear points then
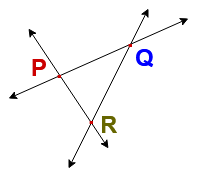
Number of lines through P, Q and R non-collinear points = 3 ( ,
,
)
Let consider P, Q, R & S are non- collinear points then
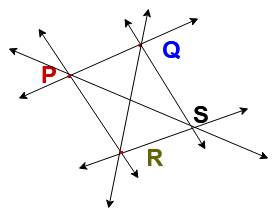
Number of lines through P, Q , R & S non-collinear points = 6 ( ,
,
,
,
,
)
Number of lines through “n” non-collinear points =

Related Topics
Two dimensional shapes formulas.
Quadrilateral Properties | Trapezium, parallelogram, Rhombus
Types of Triangles With examples | Properties of Triangle
Properties of circle in math | Arc, Perimeter, Segment of circle
Thanks for reading. I Hope you liked this article “Point in Math | Collinear Points | Non-collinear points”. Give feed back, comments and please don’t forget to share it.





