In this article we can learn about types of pyramids and geometrical formulas of surface area and volume and its properties.
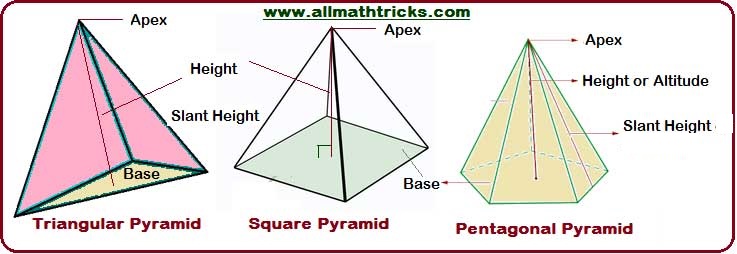
A pyramid is a three dimensional solid shape which can have any polygon as its base and its edges converge a single vertex or apex.
Its dimensions are defined by dimensions of the polygon at its base and length of its lateral edges which lead to the vertex.
Types of Pyramid
Triangular pyramid, Square pyramid & Pentagonal pyramid
The type of the pyramid is called to according to its base.
The base is triangle type then it is called Triangular pyramid.
If the base is square type then it is called Square pyramid.
If the base is pentagonal type then it is called Pentagonal pyramid.
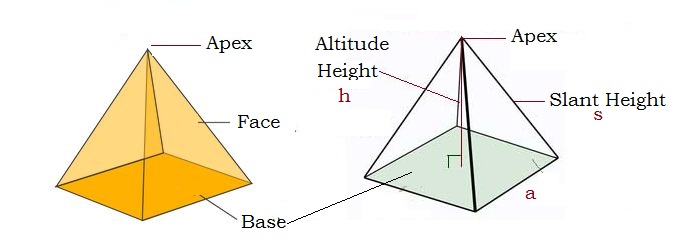
Perimeter of a pyramid (p) : It is a distance around the base of the pyramid.
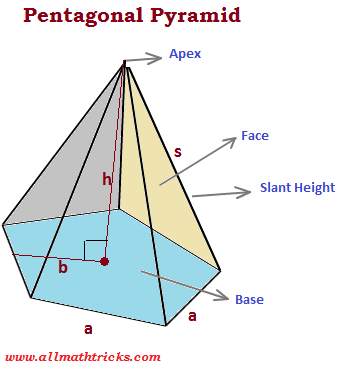
Slant height of a pyramid ( l) : It is a diagonal height from the vertex to center one of the base edges.
Height/Altitude of pyramid ( h) : Altitude ( h) is the perpendicular distance between the apex and bases of a pyramid.
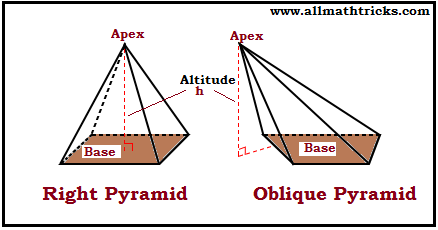
Right Pyramid & Oblique Pyramid
Right Pyramid – The Vertex or apex of the pyramid is directly above the center of its base, then it is called right pyramid.
i.e The apex line is perpendicular to its center point of its base.
The square pyramid, triangular pyramid are examples of a right pyramid.
Oblique Pyramid – The Vertex or apex of the pyramid is not having directly above the center of its base, then it is called Oblique pyramid. The face of the oblique pyramid is not congruent.
Basic Pyramid Geometrical formulas
Slant surface or lateral surface area of the pyramid (S)
Total surface area of the pyramid (SA)
SA = Lateral surface area of the pyramid + Base are of pyramid
Volume of the pyramid (V)
Triangular Pyramid
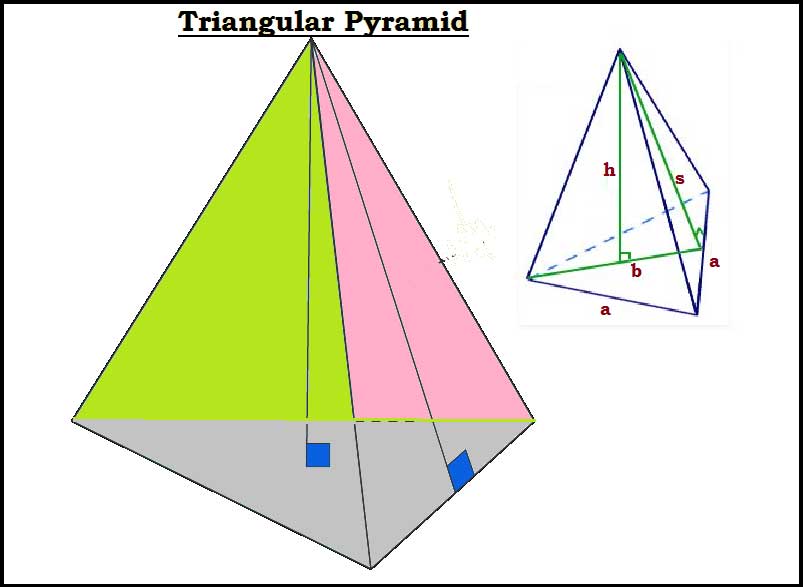
A triangular pyramid is a polyhedron with a triangular base and the three faces of the triangular pyramid meet at a point known as apex. The triangular pyramid has
A triangular pyramid has one triangular base and three triangular faces, Six edges & Four vertices
The base, faces, edges and vertices are the same for an irregular triangular pyramid or a regular triangular pyramid.
Here,
Height of the triangular pyramid – h
Slant height of the triangular pyramid – s
Base length of the triangular pyramid – a
Surface area and volume of a triangular pyramid
Base Area of a Triangular Pyramid
A =
Surface Area of a Triangular Pyramid (SA)
SA =
SA =
Volume of a Triangular Pyramid (V)
V =
V =
V =
Square Pyramid
A square pyramid is square based three-dimensional geometrical figure. All the four sides are triangular and they are meet at one single point known as apex.
A Square pyramid has
a) Five Faces
b) Four Side Faces are Triangles
c) Square Base
d) Five Vertices (corner points)
e) Eight Edges
Base Area of square pyramid (A)
A = a2
Slant surface or lateral surface area of the pyramid (S)
S= 1/2 x 4a x s = 2as
Surface area of square pyramid (SA)
SA = a2 +2as
Volume of a Square Pyramid (V)
Where ” s ” is the slant height, “a” is the base length and “h” is the height of the of the square pyramid
Pentagonal Pyramid
A pentagonal pyramid is a pyramid having a pentagonal base.
A Pentagonal pyramid has
Five triangular face
Pentagonal base
Six Faces
Six Vertices (corner points)
Ten Edges
Volume of a pentagonal pyramid (V)
Surface Area of a Pentagonal Pyramid (SA)
SA = 5/2 × a(b + s)
Hexagonal Pyramid – A hexagonal pyramid is a pyramid having a hexagonal base. It has a total of 6 sides and 6 triangular lateral faces. A hexagonal pyramid is also known as heptahedron.
| Pyramid name | Faces | Edges | Vertices |
| Triangular Pyramid (or) Tetrahedron | 4 | 6 | 4 |
| Square Pyramid | 5 | 8 | 5 |
| Pentagonal Pyramid | 6 | 10 | 6 |
| Hexagonal Pyramid | 7 | 12 | 7 |
| Heptagonal Pyramid | 8 | 14 | 8 |
| Octagonal Pyramid | 9 | 16 | 9 |
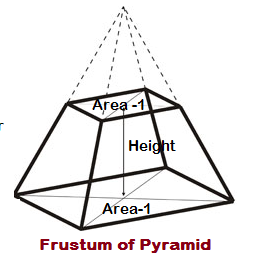
Frustum of Pyramid
When a pyramid is cut the left over part is called the frustum of a pyramid
Slant surface of the frustum of a pyramid (S)
S = 1/2 x sum of perimeter of the ends x slant height
Volume of the frustum of a pyramid (V)
V=
Where ‘h’ is the height or thickness A1 & A2 are the areas of ends of pyramid
Related Articles:
Frustum of cone formulas with examples
Centroid of the triangle formula with examples
Cone formulas – Surface Area and Volume
Surface Area and Volume of a Prism Formulas
Cylinder Formulas – Volume and Surface Area
Sphere, Hemisphere, Hollow Sphere Formulas – Surface Area and Volume
Quadrilateral formula for area and perimeter
Formulas for Arc, Perimeter, Segment of circle