Volume and Surface Area of a Cylinder Formulas

In this article provided formulas of Surface Area and Volume of a Right circular cylinder , Oblique Cylinder & Hollow Cylinder with examples

Formulas for Right circular cylinder, Oblique Cylinder & Hollow Cylinder

Cylinder Definition

A cylinder is a solid which has both its ends in the form of a circle. Its dimensions are defined in the form of the radius of the base (r) and height ( h).

i.e The lateral surfaces are curved and ends are congruent circles

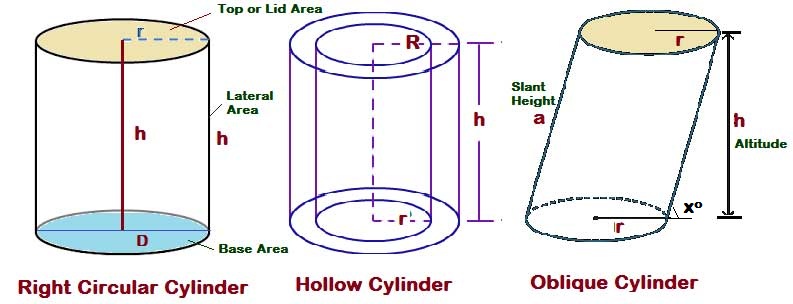
Right circular cylinder

A The line joining the centers of the circular bases is perpendicular to base, solid figure is called right circular cylinder.

Surface Area & Volume of a Right circular cylinder

Curved surface area of the right circular cylinder = Perimeter of the base of the cylinder X height

Perimeter of the base of the cylinder = Perimeter of circle with same radius = 2 π r

Curved Surface Area of Cylinder = 2 π r h

Total surface area of the right circular cylinder = Curved Surface Area of Cylinder + Base area + Top area

Base area = Top area = Area of the circle with same radius = π r²

= 2 π r h + π r²+ π r²

= 2 π r ( r + h)

Total Surface Area of Cylinder = 2 π r ( r + h)

Volume of a cylinder = Area of the circular base X height = π r²X h

Volume of a Cylinder = π r²h

Oblique Cylinder

A The line joining the centers of the circular bases. The cylinder is sideways and the axis is not a right angle to the base, then it is called an oblique cylinder.

Its dimensions are defined in the form of the radius of the base (r) and lateral height or perpendicular height or altitude ( h), Slant height ( a), angle ( x)

Surface Area & Volume of an oblique cylinder

Perpendicular height of a Oblique Cylinder

h = a sin x

Lateral or Curved surface area of a Oblique Cylinder ( A_a )

A_a = 2 π r a

Total Surface Area of Oblique cylinder ( A_s )

Total Surface Area of Cylinder = 2 π r ( r + a)

Volume of Oblique Cylinder is the same as for the Right circular cylinder

Volume of a Oblique Cylinder = π r²h = π r²a sin x

Hollow Cylinder

A hollow cylinder is the figure in shape formed by just the lateral surface of the cylinder.

i.e A Hollow cylinder can be defined as, It is a solid bounded by two co-axial cylinders of the same height

Its dimensions are defined in the form of the radius of the base outer (R) , Inner ( r) & height ( h)

Surface Area & Volume of a hollow cylinder

Curved Surface of hollow cylinder = Outer surface area of the cylinder + Inner surface area of cylinder

= 2 π R h + 2 π r h

Curved Surface of hollow cylinder = 2 π h ( R + r)

Total surface area hollow cylinder = Outer surface area of the cylinder + Inner surface area of cylinder + Area of a base circular ring + Area of a top circular ring

= 2 π R h + 2 π r h + (π R²– π r² ) + (π R²– π r²)

= 2 π h ( R + r) + 2 π ( R²– r²)

Total surface area hollow cylinder = 2 π ( R + r) (h + R – r)

Volume of the material used for hollow cylinder = Volume of the cylinder with outer radius – Volume of the cylinder with inner radius

Volume of the material for hollow cylinder = π R²h – π r²h = π h ( R² – r²)

Examples on surface area and volume calculation of cylinder

Example-1 : In a cylinder volume (v) = 176 cm³ , h = 14 cm, then find the radius of cylinder

Solution: Let the radius of cylinder = r , Then

Volume of cylinder = 176 = π r²h

⇒ π r²(14) = 176

⇒ r²= 4

⇒ r= 2

Example-2 : 15 number of identical spheres are melted and converted into cylinder shape of 10 cm radius and 5.4 cm height is made. Then find the radius of sphere.

Solution: Let the radius of spheres = r

Total volume of spheres = Volume of resultant cylinder

⇒ 15 x (4/3) x π x r³= π x (10)²x 5.4

⇒ r³= 27

⇒ r= 3 cm

Example-3: The diameter of a garden roller is 0.7 m and it is 2 m long. Then find area covered by it in 10 revolution.

Solution: Garden roller covered in one revolution = Curved Surface Area of roller

Here dia of roller (D)= 0.7 m and long (h) = 2 m

i.e Lateral surface area of the garden roller = π D h = (22/7) x 0.7 x 2 = 4.4 m²

For 10 revolutions = 10 x 4.4 = 44 m²

Example-4: A hollow pipe long 20 cm, outer dia is 25 cm and thickness of the metal 1 cm. Find the total surface area of the pipe

Solution: Here radius of outer shell = R = 25/2 = 12.5 cm

Length = h = 14 cm

Thickness of pipe = R -r = 1 cm

Inner shell radius = r = 12.5 – 1 = 11.5 cm

Total surface area of the pipe = 2 π ( R + r) (h + R – r)

= 2 x ( 22/7) x ( 12.5 + 11.5 ) x ( 20 + 1) = 3168 cm²

Example-5: The height of a metallic hallow cylinder is 14 cm and difference between its inner curved surface area and outer curved surface area is 44 cm². If the cylinder is made up of volume 99 cm³ metal. Find its inner & outer radius.

Solution: Let radius of outer shell = R & inner shell radius = r

Length = h = 14 cm

Here difference between its inner curved surface area and outer curved surface area is 44 cm²

i.e ⇒ 2 π R h – 2 π r h = 44

⇒2 x (22/7) x 14 (R – r) = 44

⇒ R – r = 1/2 ————————- (Eq- 1)

Volume of cylinder = 99 cm³

i.e

⇒ π h ( R² – r²) = 99

⇒ π x 14 x ( R + r ) (R -r) = 99

From the equation – 1

⇒ R + r = 9/2 ——————– (Eq- 2)

Simplifying the eq-1 & eq-2

R = 5/2 cm & r = 2 cm

Example-6: A well of 14 m base radius is digged soil upto a depth of 10 m and from this soil material was made 7 m wide platform around the well. Find the height of platform

Solution: Here Well radius r₁ = 10 m , Depth of well h₁ = 10 m platform radius inner r = 14 m , outer radius = 21 m, height of the plat form = h

⇒ Volume of well = Volume of plat form

⇒ π r₁²h₁ = π h ( R² – r²)

⇒ π x 14 x 14 x 10 = π x h x (21² – 14² )

⇒ 14 x 14 x 10 = h x (21+14) x (21-14)

⇒ h = 8

Thanks for reading this article. I Hope you liked this article “ Volume and Surface area of a cylinder like Right circular cylinder , Oblique Cylinder and Hollow Cylinder formulas”. Give feed back and comments please.