In this article provides the simple tricks with formulas to find the number of triangles for the following figures
- Counting triangles with in Square, Rectangle, Quadrilateral
- Number of possible triangles within a triangle
How to Calculate Number of Triangles in a Square | Trick to Count no of Triangles
Calculate number of triangles in a square
Type – 1 : Counting triangles with in Square, Rectangle, Quadrilateral
Find the number of triangles in the above figures
Figure – 1 : Number of triangles in Fig – 1 = 8
Hint: Here having total two diagonals and having four blocks. So formula for that 4 x 2 = 8 number of triangles.
Figure – 2 : Number of triangles in Fig – 2 = 16
Hint: Here having total two diagonals and having eight blocks. So formula for that 8 x 2 = 16 number of triangles.
Figure – 3 : Number of triangles in Fig – 3 = 18
Hint: Here each square having 8 no. of triangles and combine squares having 2 no. of triangles. So total number of triangles – 8 + 8 + 2 = 18.
Figure – 4 : Number of triangles in Fig – 3 = 28
Hint: Here each square having 8 no. of triangles and combine squares having 4 no. of triangles. So total number of triangles – 8 + 8 + 8 + 4 = 28.
Trick to count no of triangles : Intersection of diagonals in a square, rectangle, rhombus, parallelogram, quadrilateral and trapezium will give eight triangles.
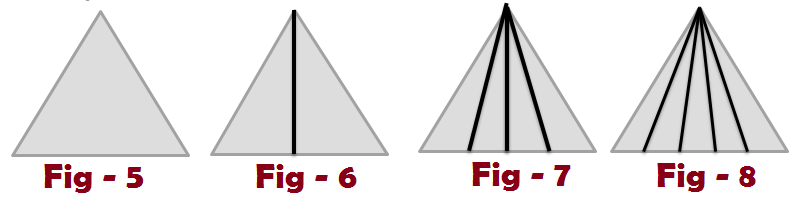
Type – 2 : Counting triangles with the Triangle having number of bisects with vertex
Count the number of possible triangles in the above figures
Figure – 5: Number of possible triangles in Fig – 5 = 1
Figure – 6 : Number of possible triangles in Fig – 6 = 3
Formula : Here number of parts ” n” then possible triangles is n (n+1) /2
Figure – 7 : Number of possible triangles in Fig – 7 = 10
Hint : No of parts ” n” = 4 so according to formula 4 x 5 /2 = 10
Figure – 8 : Number of possible triangles in Fig – 8 = 15
Hint : No of parts ” n” = 5 so according to formula 5 x 6 /2 = 15.
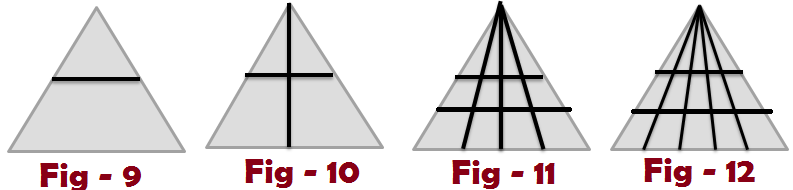
Type – 3 : Counting triangles with the Triangle having number of bisects with vertex and horizontal lines
Count the number of triangles in the above picture
Figure – 9: Triangle counting in Fig – 9 = 2
Figure – 10: Triangle counting in Fig – 10 = 6
Formula : Here number of vertical parts ” n” and horizontal parts “m” then possible triangles is
Figure – 11: Triangle counting in Fig – 11 = 30
Solution : Here number of vertical parts ” 4″ and horizontal parts “3” then possible triangles is 4 x 3 x 5 /2 = 30
Figure – 12: Triangle counting in Fig – 12 = 45
Solution : Here number of vertical parts ” 5″ and horizontal parts “3” then possible triangles is 5 x 3 x 6 /2 = 45
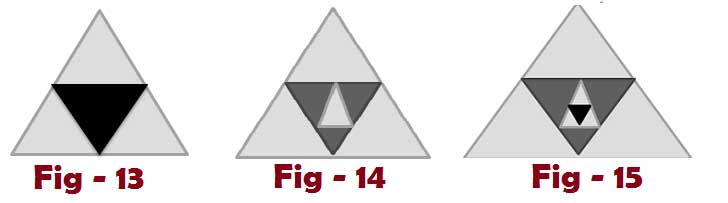
Type – 4 : Counting triangles with in embedded Triangle
How many triangles are in the above figures
Figure – 13: Triangle counting in Fig – 13 = 5
Formula : Here number embedded triangles in outer triangle ” n” and horizontal parts “m” then possible triangles is 4n + 1
Figure – 14: Triangle counting in Fig – 14 = 9 ( Here n= 2 )
Figure – 15: Triangle counting in Fig – 15 = 13 ( Here n= 3 )
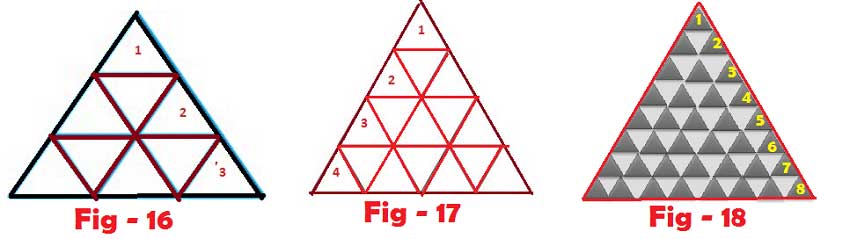
Type – 4 : Counting triangles with in the particular pattern of Triangle
How many possible triangles are in the above figures
Formula to count number of triangles like above particular pattern type of Triangle
where “n” = number of unit triangles in a side
Note : Consider only integer part from answer obtained in above formula ( For example the answer may come 13.12 then consider only “13”. Also remember You don’t have to round off the number for example answer may come 36.8 then consider only “36”.
Figure – 16: No of triangles in Fig – 16 = 13 ( Here n= 3 )
Solution: According to above formula 3 x 5 x 7 /8 = 13.12 so consider integer only i.e 13
Figure – 17: No of triangles in Fig – 17 = 27 ( Here n= 4 )
Solution: According to above formula 4 x 6 x 9/8 = 27
Figure – 18: No of triangles in Fig – 18 = 170 ( Here n= 8 )
Solution: According to above formula 8 x 10 x 17/8 = 170
Related Articles:
Multiplication tricks for easy calculations | Math Tricks
Speed Math Division Shortcut tricks
Easy methods for Cube of a Number | cube of a number calculator
Square root calculation methods | square root formulas
We hope this page “Trick to count no of triangles” fulfill your requirement. Please give feed back, comments to improve this and don’t forget to share this page.





38 thoughts on “Find the Number of triangles in the given figure | Count the number of triangles”
Shashi Totad
(November 17, 2018 - 4:53 am)U people r just awesome… I was literally struggling to solve these problems in my police sub-inspector exams… But now I just spent 30 min …Ready to solve complex problems..Thanks a ton for ur genuine efforts…way to go keep up the same work going on.
Regards,
Shashi
sivaalluri
(November 18, 2018 - 2:04 pm)Thank you Mr.Shashi Totad for your valuable comments
Avika
(January 25, 2022 - 1:55 pm)Best Website for Reasoning Preparation
sivaalluri
(February 2, 2022 - 1:12 am)welcome
Suresh
(January 4, 2019 - 5:19 pm)Super
sivaalluri
(January 27, 2019 - 4:10 am)Thank you
Om Namah Sivay allurian
(February 7, 2019 - 4:12 am)Thanks a lot for the tricks.
They are used in all competitive exams.
sivaalluri
(February 20, 2019 - 3:26 pm)Thank you
sai manne
(March 26, 2019 - 7:13 am)This is the best website to learn to count no. of triangles lesson. Because most of the websites I’ve seen are showing wrong and different answers for the same question. Finally, I am here happy to find valid and correct answers, and also methods to do it in the right way. Thanx a lot.
sivaalluri
(April 6, 2019 - 2:38 pm)Thank you Mr.Sai for your valuable comment on this article
S. Chidambaranathan
(April 7, 2019 - 12:49 am)Really loved it. I really wanted this. But please make your website secure
sivaalluri
(April 20, 2019 - 3:14 pm)Thank for your suggestion
Sagarika
(October 23, 2019 - 3:37 pm)Thanks lot
sivaalluri
(October 27, 2019 - 3:34 am)welcome sagarika
devendra
(May 3, 2019 - 8:17 pm)hello sir ,
your blog for these tricks is really helpful for me.
i just want to how we can find no .of triangles in triangle when it has three medians intersect each other
sivaalluri
(May 10, 2019 - 3:43 pm)Please go through the below link
Number of triangles in a figure telugu | number of triangles in a triangle in telugu | Count triangles in telugu
https://youtu.be/2RPCPQC24k4
devendra
(May 3, 2019 - 8:26 pm)sir ,
it seems that Type -3 formula fails in case if horizantal and vertical lines are same in a triangle
sivaalluri
(May 10, 2019 - 3:47 pm)no it works well
shyam
(June 2, 2019 - 6:04 pm)bro for this your assumption and tricks are good to solve but what to do when all the above are jumbled to single diagram ……or some another diagram (example is civils prelims triangle sum )
sivaalluri
(June 4, 2019 - 2:46 pm)Ok we will correct it
Hitler
(December 27, 2019 - 8:30 am)Thanks
sivaalluri
(December 29, 2019 - 1:59 pm)Welcome
Aayush
(January 18, 2021 - 3:44 pm)Very nice and helpful tricks. Can you please add their derivations also? I have derived some of them using combinatorics. Need help in derivations of others.
MOIN KHAN
(April 24, 2020 - 1:52 am)Bhai Mza aa gay…….
sivaalluri
(April 26, 2020 - 11:23 am)Welcome
Chukwuma
(September 16, 2021 - 8:37 pm)Thanks so much, I have learnt alot from you guys.
sivaalluri
(September 18, 2021 - 5:33 am)welcome
Kavya
(December 19, 2021 - 4:35 pm)Thanks for your efforts sir. Many people will be benefitted. Please keep going sir 🙂
sivaalluri
(January 2, 2022 - 8:48 am)Thanks for your compliment
raj
(December 20, 2021 - 5:28 pm)You guys are wonderful. Thanks bro
sivaalluri
(January 2, 2022 - 8:49 am)welcome
Tony G. Parkes
(March 1, 2022 - 8:21 pm)thanks you for such a awesome blog it is gonna to be really helpful
SHREYANSH
(May 11, 2022 - 5:18 am)11 th question under how become 3rd horizontal
Forpenz
(May 22, 2023 - 12:35 am)This is amazing, I have been helped.
Forpenz Anthony
(May 22, 2023 - 12:38 am)This is amazing, I have been struggling for a long time, now I can breath.
sivaalluri
(June 14, 2023 - 4:06 am)Welcome
Bekas
(March 24, 2024 - 5:35 am)Nice and helpful post
sivaalluri
(April 12, 2024 - 5:14 am)Welcome