Square Root calculation methods | square root formulas
Definition of square root: Mathematically, it is defined as the ” square root of a number is a value that, when multiplied by itself, gives the number”. i.e. When a number is multiplied by itself to give the square of number then that number is a square root for that square number. Square root represented by a symbol ” √ “
Now we learn different methods for finding the square root
a) Square Root of any number by the long division method. (It is a general method for square root calculation).
b) Square Root of a Perfect Square by using the Prime Factorization Method.
c) Shortcut trick for finding the square root for the perfect square number.
d) Approximate Square Root of any number which is not a perfect square.
Square root of any number by the long division method.
Here explain with examples step by step.
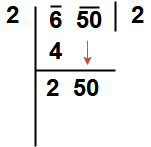
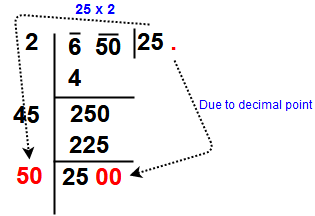
Take an example Find √650 to one decimal place.
Step 1: The given number to be group the digits in pairs, and the remaining digit (if any) is called a period.
Here is our given number 650. So it is grouped as 6 – 50
Step 2 : Find the largest number whose square is equal to or just less than the first period or pair. Here Square the 2, giving 4, and Square the 3, giving 9. So write 4 that underneath the 6. Take the number ‘ 2 ” as the divisor and also as the quotient.
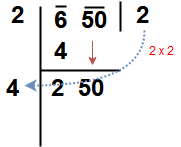
Step 3 : Now take Subtract the product of the divisor and the quotient (i.e. 2 x 2 = 4) from the first period or pair ( i.e 4). Bring down the next pair of digits and this becomes the new dividend.
Step 4: Now, the new divisor is obtained by taking two times the quotient. Here quotient is 2 so the new divisor 2 x 2 = 4 and the new dividend is 250.
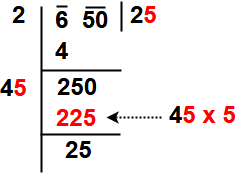
Step 5: Now think suitable single-digit number which is also taken as the next digit of the quotient. The single digit is to be choose like the product of product of the new divisor and the this single digit to be equal to or just less than the new dividend.
Here check one by one digit i.e 41 x 1 = 41 , 42 x 2 = 84, 43 x 3 = 129, 44 x 4 = 176, 45 x 5 = 225, 46 x 6 = 275 . So take the single digit is 5.
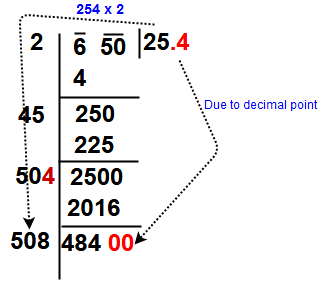
Step 6 : Subtract and bring down the next pair of digits to dividend. So here not having the pairs so put the decimal in the quotient place and drop down digits 00. The new divisor is obtained by taking two times the quotient. Here quotient is 25 so the new divisor 2 x 25= 50 and the new dividend is 2500.
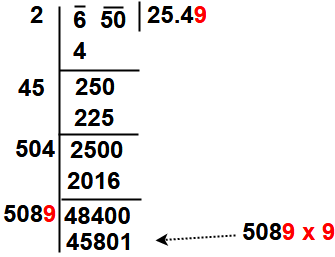
Now Repeat steps (4), (5)and (6) till all the periods have been taken up. Finally the quotient so obtained is the required square root of the given number.
So our final answer is √650 = 25.49 = 25.5.
Square Root of a Perfect Square by using the Prime Factorization Method.
This method applicable only the to the perfect square root numbers
Step1 : Write the given number into prime factors.
Step2 : Make pairs of similar factors.
Step 3 : Take the product of prime factors, then choose one factor out of each pair.
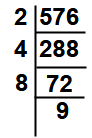
Example: Find the Square root of 576 by prime factorization method.
Factors of 576 = 2 x 4 x 8 x 9
Prime Factors of 576 = 2 x 2 x 2 x 2 x 2 x 2 x 3 x 3
Collect the one factor out of each pair i.e = 2 x 2 x 2 x 3 = 24
So √576 = 24.
Shortcut trick for finding the square root for the perfect square number.
This method applicable only for the perfect square root numbers
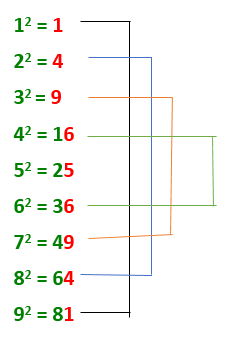
Remember the following table ( i,e squares of 1 to 9 numbers) and given simple logic.
-
- If the last digit of the perfect Square number =1, the last digit of the Square root for that number=1 or 9.
- If the last digit of the perfect Square number =4 , the last digit of the Square root for that number 2 or 8.
- If the last digit of the perfect Square number =9, the last digit of the Square root for that number=3 or 7.
- If the last digit of the perfect Square number =6, the last digit of Square root for that number=4 or 6.
- If the last digit of the perfect Square number =5, the last digit of Square root for that number=5.
Take example
Ex. 1: Find the square root of 7056.
Step 1: The given number is to be grouped the digits in pairs, and the remaining digit (if any) is called a period. Write two digit parts i.e 70 – 56 and the Lost digit is ” 6 ” so the last digit of the Square root for that number=4 or 6.
Step 2 : Leave the first two digits and take the next remaining digits. Here the remaining number is ” 70″.
Step 3 : Find the less square number for ” 70″ .
i.e 82 < 70 < 92
So Take the less number i.e ” 8″ . Here our next digit of the square root is ” 8 “
Step 4 : The square root of 7056 is 84 or 86.
Step 5 : Take the second digit in the square root (i.e 8 ) and multiplying it, by the next preceding number (i.e 8 x 9 = 72 ).
Step 6 : Compare the multiplied value ( i.e 72) with the 2nd part of the number (i.e 70 ).
If the 2nd part of the number is high then take a big number.
If the 2nd part of the number is less then take a small number.
Here ( 2nd part of the number) 70 < 72 . So take the small number 84 from 84 and 86.
Square root of 7056 is 86.
Ex. 2 : Find the square root of 784
Step 1 : Separate the number into two digits (i. e 7 – 84) and Identify the lost digit of the number. Here lost digit is ” 4″ so the last digit of the Square root for that number = 2 or 8.
Step 2 : Leave the first two digits and take the next remaining digits. Here remaining the number is ” 7″.
Step 3 : Find the less square number for ” 7″ .
i.e 22 < 7 < 32
So Take the less number i.e ” 2″ . Here our next digit of square root is ” 2 “
Step 4 : The square root of 784 is 22 or 28.
Step 5 : Take the second digit in square root (i.e 2 ) and multiply it by the next preceding number (i.e 2 x 3 = 6 ).
Step 6 : Compare the multiplied value ( i.e 6) with the 2nd par of the number (i.e 7 )
Here 7 > 6 . So take height number 28 from 22 and 28.
Square root of 784 is 28.
Approximate Square Root of any number which is not a perfect square.
The formula in this method :
Square Root of the number = Square Root of Nearest Perfect Square + { [ difference of the given number from the nearest perfect square] / [ 2 x Square root of Nearest Perfect Square]
For example,
Find the Square Root of 650.
Sol : The perfect square closest to 625 is 25; we will take the square root of 625 i.e. 25 in this calculations
= 25 +[ (650-625) / (2 x 25) ]
= 25 + [ 25 /( 2×25)]
=25 + 0.5
= 25.5 (approximate value).
Find the Square Root of 1009.
perfect square closest to 1009 is 32; we will take the square root of 1024 i.e. 32 in this calculations
= 32 – [ (1024-1009) / (2 x 32) ]
= 32 – [ 15 /( 2×32)]
=32 – 0.23 = 31.77 (approximate value).
Cube Root formula of Perfect Cubes of 1 to 100 | Cube root formula in math
Easy Addition and Subtraction Tricks | Shortcut Process for addition
Shortcuts for Multiplication of numbers | Easy way for Multiplications
Percentage formulas while increase and decrease percent of a number
Easiest way to find square of a 2 digit number | Shortcut trick for Square
Shortcut Methods for finding the Cube of a number | number cube tricks
Cube Root formula of Perfect Cubes of 1 to 100 | Cube root formula in math
Shortcuts methods of Division math | Tips and tricks for math division
Hi friends Thanks for reading. I hope you like it. Give feedback, comments and please don’t forget to share it
