Highest Common Factor and Lowest Common Multiple | HCF and LCM

Factorization and Division Methods for finding  HCF and LCM

Terminology in  concepts of HCF (Highest Common factor) or LCM(Lowest Common Multiple) :

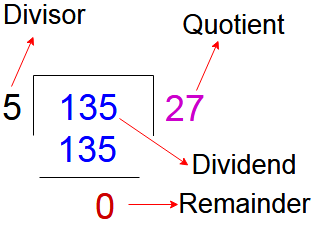
• Divisor
• Dividend
• Quotient
• Remainder
• Multiple
• Divisible

Factor or Divisor : A factor or divisor of a positive integer and it is divides it evenly parts of any  positive integer ( i.e remainder is zero ).

For example the factors of 12 are 1, 2,3,4,6 and 12.

A common factors of “n1” and “n2” are the numbers. Now any number “x” is a factor of “n1” and also factor of “n2” then “x” is called common factor of n1 ans n2.

Ex: 6 is a common factor of 12 and 24.

Divisible

If n1 and n2 are two numbers

n1 is divisor , n2 is dividend and remainder came zero than n1 is divisible or factor of n2

For example 2, 3,4,6,8,12 are  divisors or factor of 24.

The word ” divisible appears in a question, it means ” it divides equal parts or divisible without remainder.

Multiple:

A multiple of an integer N is any integer that is evenly divisible by M

If take numbers n1, n2, n3, n4, n5 and x is the common divisible number for all these numbers

Than multiples of the number ” x ” are  n1, n2, n3, n4 & n5

For example 10,15,20,25,30,35,40 …….. are multiples of 5

HCF (Highest Common factor) or GCD(Greatest Common Divisor):

HCF of two or more than numbers is the greatest number (divisor) that divides all the given number exactly. So HCF is also called the greatest common divisor(GCD).

Suppose If numbers n1 and n2 are exactly divisible by the same numbers x, than x is a common divisior of n1 and n2. Now highest number of all the common divisiors of n1 and n2 is called the GCD of HCF .

Some important tips on HCF

• For two no. n1 and n2 if n1 < n2 then HCF of n1 and n2 is always less than or equal to n1 .
• The greatest number by which n1, n2 and n3 completely divisible is the HCF of n1, n2 and n3.
• The greatest number by which x, y, z divisible and gives the remainder a, b and c is the HCF of (x –a), (y–b) and (z–c).
• If the HCF of x and y is n, then the HCF of numbers { x, (x+y)} and {x, (x-y)} are also G
• The greatest number by which x, y and z divisible and gives same remainder in each case, that number is HCF of (x–y), (y–z) and (z–x).

There are two methods to find the Highest Common Factor (HCF)

Division method

Let we have three numbers .Pick the smaller one and divide it by the larger one. After that divide the divisor with the remainder. This process of dividing the preceding number by the remainder will repeated until we got the zero as remainder.The last divisor is the required H.C.F.

Example : 1

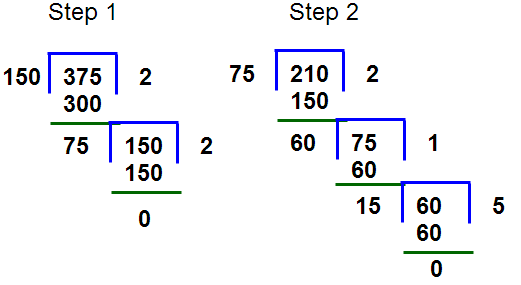
Find the HCF of 150,210 and 375.

Step 1 : Take highest  and lowest number i.e  375 and 150

Step 2 : Division the number 375 by 150 than quotient 2 , dividend 300 and remainder 75.

Step 3 : The divisior 150 comes to divident place and remainder 75 act as a divisor than here quotient comes 2 and remainder having “0”.

So HCF for the numbers 150 and 375 is 75

Step 4 : Now take numbers 75 and 210 than follow the above process until we got the  remainder as zero.

Step 5 : Divisior = 75 , Dividend = 210 , quotient = 2 and remainder = 60

Step 6 : Divisior = 60 , Dividend = 75 , quotient = 1 and remainder = 15

Step 7 : Divisior = 15 , Dividend = 60 , quotient = 4 and remainder = 0

So Finally the HCF of the numbers 150, 210 & 375 is 15.

Example : 2

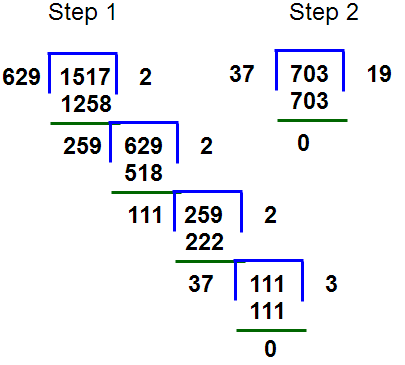
Find the greatest number that will divided 640, 710 and 1526 so as to leave 11,7 &9 as a remainders respectively.

Step 1 : Subtract all numbers with there respective remainders i.e 640-11=629, 710-7=703 and 1526-9=1517.

Step 2 : Take 629 and 1517 and follow the division methods

Step 3 : Divisior = 629 , Dividend = 1517 , quotient = 2 and remainder = 259

Step 4 : Divisior = 259 , Dividend = 629 , quotient = 2 and remainder = 111

Step 5 : Divisior = 111 , Dividend = 259 , quotient = 2 and remainder = 37

Step 6 : Divisior = 37 , Dividend = 111 , quotient = 3 and remainder = 0

Step 7 : Now take 37 and 703 than follow the division methods i.e Divisior = 37 , Dividend = 703, quotient = 19 and remainder = 0

So finally the HCF of  the numbers 629,703,1517 is 37.

Factor method (Prime factors methods)

Steps for finding HCF of two numbers x and y

• Write out the all prime factors that are common to the standard forms of the numbers x and y.
• Raise each of the common prime factors listed above to the lesser of the powers in which it appears in the standard forms of the numbers “x” and “y”
• The product of the results of the previous steps will be the GCD of x and y

Example : 3

Find the HCF of 150,210 and 375.

Step 1 : Write down the standard form of numbers

i.e 150 = 5 x 5 x 3 x 2 = 5² x 3¹ x 2¹

210 = 5 x 2 x 7 x 3 = 5¹ x  7¹ x 3¹ x 2¹

375 = 5 x 5 x 5 x 3 = 5³ x 3¹

Step 2 : Write the prime factors common to all the three numbers is 5¹ x 3¹ ( Here powers of the numbers to be take lowest values)

Step 3 : So HCF of the numbers 150, 210 and 375 is 15 ( 5 x 3 = 15)

Example : 4

Find the greatest numbers which will divide 321, 428 and 535 exactly.

Step 1 : Write down the standard form of numbers

i.e 321 = 3 x 107 = 3¹ x 107¹

428 = 2 x 2 x 107 = 2² x  107¹

535 = 5 x 107 = 5¹ x 107¹

Step 2 : Write the prime factors common to all the three numbers is 107¹ ( Here powers of the numbers to be take lowest values from all the common prime factors)

Step 3 : So HCF of the numbers 321, 428 and 535 is 107

LCM (Lowest Common Multiple)

LCM is the least dividend which is exactly divisible by given numbers.

Suppose If numbers n1 and n2 are two numbers distinct from each other. The smallest natural number “x” that is exactly divisible by n1 and n2 than “x” is called least common multiple (LCM) of n1 and n2.

Some important tips on LCM
For two numbers x and y if x < y, then L.C.M. of x and y is more than or equal to y.

If ratio between two numbers is x : y and their H.C.F. is n, then their L.C.M. = xyn.

If ratio between two numbers is x : y and their L.C.M. is n, then their H.C.F = ( n / xy)
The smallest number which is divided by x, y and z give remainder a, b and c, but (x – a) = (y – b) = (z – c) = n, then number is  L.C.M. of (x, y and z) – n).
The smallest number which is divided by x, y and z give remainder n in each case, then number is (L.C.M. of x, y and z) + n.

There are two methods to find the LCM

1. Division method

Let we have set of numbers. First of all find the number which divide at least two of the number in a given set of number.remainder and not divisible numbers will carry forward as it is. Repeat the process till at least two number is not divisible by any number except 1. The product of the divisor and the undivided numbers is the required L.C.M.

Example 5: Find the LCM of numbers 72, 108 & 2100

LCM of the numbers 72, 108 and 2100  = 2 x 6 x 3 x 2 x 3 x 175 = 37800

Example 6 : Find the LCM of numbers 12, 15, 20 & 27

LCM of the numbers 12, 15, 20 & 27 =  2 x 5 x 3 x 2 x 9 = 540

2. Factor method (Prime factors method)

Steps for finding LCM of two numbers x and y

• Write out the all prime factors that are common to the standard forms of the numbers x and y.
• Raise each of the common prime factors listed above to the highest of the powers in which it appears in the standard forms of the numbers “x” and “y”
• The product of the results of the previous steps will be the LCM of x and y

Example 7 : Find the LCM of numbers 72, 108 & 2100

Step 1 : Write down the standard form of numbers

72 = 2³ x 3²

108 = 2² x 3³

2100 = 2³ x 3³ x 5² x 7¹

Step 2 : Write each of the prime factors to their highest available power.

i.e 2³ x 3¹ x 5² x 7¹  = 37800( Here consider all prime numbers)

Step 3 : So LCM of the numbers 72, 108 & 2100 is 37800.

Example 8 : Find the LCM of numbers 12, 15, 20 & 27

Step 1 : Write down the standard form of numbers

12 = 2² x 3¹

15 = 5¹x 3¹

20 = 5¹ x 2²

27 = 3³

Step 2 : Write each of the prime factors to their highest available power.

i.e 2² x 3³ x 5¹  = 540( Here to be consider all prime numbers)

Step 3 : So LCM of the numbers 12, 15, 20 & 27 is 540.

Formula for finding HCF and LCM of fractions.

1. HCF of two or more fractions is given by

2. LCF of two or more fractions is given by

The Product of the LCM and the HCF equals the product of the numbers

I.e a and b are two numbers and its HCF and LCM are n & m respectively  then  a x b = n x m

Example 9

Find the LCM and HCF of 2.5, 0.5 & 0.175

Solution:

Step 1 : Write these numbers in fraction from i.e 2.5/10 , 0.5/10 & 175/1000

Step 2 : Write prime factors of all numbers of numerator and denominator

25 = 5²

5 = 5¹

175 = 5³ x 7¹

10 = 5¹ x 2¹

1000 = 5³ x 2³

Step  3 : Find HCF and LCM of numerator and denominator

LCM { 25 , 5 , 175 } = 5 x 5 x 7 = 175

HCF { 25 , 5 , 175 } = 5

LCM { 10, 1000 } = 1000

HCF { 10, 1000 } = 10

Step 4 : According to the above formulas we can find the answers

LCM { 2.5, 0.5 , 0.175} = 175/10 = 17.5

HCF { 2.5, 0.5 , 0.175 } = 5/1000 = 0.005

Example 10

The LCM of two numbers is 936. If their HCF is 4 and one of the number is 72, then find the other number?

Solution : Say another number “n”

Formula : LCM x HCF = Product of numbers

So 936 x 4 = 72 x n

n= 52

For more sums on GCD and LCM Problems & Solutions

Go to main page Quantitative Aptitude

Number System :

Number Categories

Rules for Divisibility of numbers

Formulas for Sum of n Consecutive numbers

Hi friends Thanks for reading. I Hope you liked it.  Give feed back, comments and please don’t forget to share it.