Divisibility Rules for easy calculations of mathematics
Here given divisibility rules for the numbers from 1 to 20.
Divisibility rules for 2, 4, 8, 16 :
Divisible by 2 : Last digit of a any number is divisible by 2 than that hole number is divisible by 2
i.e Any number end with 0,2,4,6,8 than it is divisible by 2
Divisible by 4 : A number is divisible by 4, if the number formed with its last two digits is divisible by 4.
Divisible by 8 : A number is divisible by 8, if the number formed with its last three digits is divisible by 8.
Divisible by 16 : A number is divisible by 16, if the number formed with its last three digits is divisible by 16.
Examples:
1.Check divisibility by 2, 4, 8 & 16 of the number 413984.
- The lost digit of the above number is 4. So this number is divisible by 2.
- Take lost two digits i. e 84 and 84 divisible by 4 ( 84/4 = 21). So this number is divisible by 4
- Now take lost three digits i. e 984 and 984 divisible by 8 ( 984/8 = 123). So this number is divisible by 8.
- Take lost four digits i. e 3984 and 3984 divisible by 16 ( 3984/16 = 249). So this number is divisible by 16.
2. Check divisibility by 2, 4, 8 & 16 of the number 24589436.
- The lost digit of the above number is 6. So this number is divisible by 2.
- Take lost two digits i. e 36 and 36 divisible by 4 ( 36/4 = 9). So this number is divisible by 4
- Now take lost three digits i. e 436 and 436 not divisible by 8 ( 436/8 = reminder 4). So this number is not divisible by 8.
- Take lost four digits i. e 9436 and 9436 is not divisible by 16 ( 9436/16 = reminder 4). So this number is not divisible by 16.
Divisibility rules for 3, 9 :
All such numbers the sum of whose digits are divisible by 3 are divisible by 3. In the same rule also applicable for 9 also i.e the sum of digits of a number are divisible by 9 then it is divisible by 9.
Examples :
1.Check divisibility by 3 & 9 of the number 25498644.
The sum of all digits in a given number = 2+5+4+9+8+6+4+4 = 42
So here 42 is divisible by 3 and not divisible by 9 . So given number is also divisible by 3 and not divisible by 9.
1.Check divisibility by 3 & 9 of the number 232911.
The sum of all digits in a given number = 2+3+2+9+1+1 = 18
So here 18 is divisible by 3 and also divisible by 9 . So given number is also divisible by 3 and 9.
Divisibility rules for 5 :
Any number end with 0 or 5 then it is divisible by 5.
1.Check divisibility of the number 95487430 by 5
The lost digit of the given number is “0” . So it is divisible by 5.
2.Check divisibility by 5 of the number 265474585.
The lost digit of the given number is “5” . So it is divisible by 5.
Divisibility rules for 6 :
A number is divisible by 6, if it is simultaneously divisible by 2 and 3.
Example:
1.Check divisibility by 6 of the number 357282918.
- The lost digit of the above given number is 8. So this number is divisible by 2.
- The sum of all digits in a given number = 3+5+7+2+8+2+9+1+8 = 45 and it is divisible by 3 (45/3=15).
- The given number is divisible by 2 and 3. So it is also divisible by 6.
2.Check divisibility by 6 for the number 4875614.
- The lost digit of the above given number is 4. So this number is divisible by 2.
- The sum of all digits in a given number = 4+8+7+5+6+1+4 = 35 and it is not divisible by 3 (35/3= reminder is 2)
- The given number is divisible by 2 and not divisible by 3. So the given number is not divisible by 6.
Divisibility rules for 7 :
We use oscillator (– 2) for divisibility test.
for example take number 39732
step 1 : Separate unit place from the given number and multiplied by “-2” for unit digit place ( 2 x -2 = -4) . This product is to be add for remaining number [ 3973 + (-4) = 3969].
step 2 : Separate unit place from 3969 and multiplied by “-2” for unit digit place ( 9 x -2 = -18) . This product is to be add for remaining number [ 396 + (-18) = 378].
step 3 : Separate unit place from 378 and multiplied by “-2” for unit digit place ( 8 x -2 = -16) . This product is to be add for remaining number [ 37 + (-16) = 21].
Here 21 is divisible by 7 so the given number is also divisible by 7
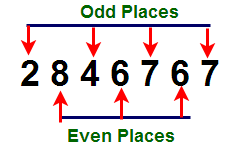
Divisibility rules for 11 :
A number is divisible by 11, if the difference of the the sum of the digits in the odd places and the sum of the digits in the even places is zero or is divisible by 11.
Examples :
1.Check the divisibility of a number 2846767 by 11.
- Odd places of the given number = 7 + 7 + 4 + 2 = 20
- Even places of the given number = 6+6+8 = 20
- The difference of the sum of odd and even places is ” 0″ . So the number 2846767 is divisible by 11.
2.Check the divisibility of a number 964712435 by 11.
- Odd places of the given number = 5 + 4 + 1 +4 +9 = 23
- Even places of the given number = 3 + 2 + 7 + 6 = 18
- The difference of the sum of odd and even places is ” 5″ . So the number 964712435 is not divisible by 11.
Divisibility rule for 13 :
We use oscillator (+4) for divisibility test of 13.
for example take number 7631
step 1 : Separate unit place from the given number and multiplied by ” 4″ for unit digit place ( 1 x 4 = 4) . This product is to be add for remaining number [ 763 + (4) = 767 ].
step 2 : Separate unit place from 763 and multiplied by “4” for unit digit place ( 7 x 4 = 28) . This product is to be add for remaining number [ 76 + (28) = 104].
Here 104 is divisible by 13 so the given number 7631 is also divisible by 13. ( If we continue the same process for next step than final value will get 13)
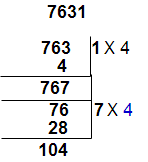 Divisibility rule for 17 :
Divisibility rule for 17 :
We use oscillator (-5) for divisibility test of 17.
for example take number 1525665
step 1 : Separate unit place from the given number and multiplied by ” -5″ for unit digit place ( -5 x 5 = -25) . This product is to be add for remaining number [ 152566 + (-25) = 152541].
step 2 : Separate unit place from 152541 and multiplied by “-5” for unit digit place ( -5 x 1 = -5) . This product is to be add for remaining number [ 15254 + (-5) = 15249 ].
step 3 : Separate unit place from 16249 and multiplied by “-5” for unit digit place ( -5 x 9 = -45) . This product is to be add for remaining number [ 1524 + (-45) = 1479].
step 4 : Separate unit place from 1579 and multiplied by “-5” for unit digit place ( -5 x 9 = -45) . This product is to be add for remaining number [ 147 + (-45) = 102].
Here 102 is divisible by 17 so the given number is also divisible by 17. ( If we continue the same process for next step than final value will get 0)
Divisibility rule for 19 :
We use oscillator (+2) for divisibility test of 19.
for example take number 112043
step 1 : Separate unit place from the given number and multiplied by ” 2″ for unit digit place ( 2 x 3 = 6) . This product is to be add for remaining number [ 11204 + (6) = 11210 ].
step 2 : Separate unit place from 11210 and multiplied by “2” for unit digit place ( 2 x 0 = 0) . This product is to be add for remaining number [ 1121 + (0) = 1121].
step 3 : Separate unit place from 1121 and multiplied by “2” for unit digit place ( 2 x 1 = 2) . This product is to be add for remaining number [ 112 + (2) = 114].
Here 114 is divisible by 19 so the given number is also divisible by 19. ( If we continue the same process for next step than final value will get 19)
Hi friends Thanks for reading. I Hope you liked it. Give feed back, comments and please don’t forget to share it.
Return to main page Quantitative aptitude math
Number System:
Formulas for Sum of n Consecutive numbers
GCD and LCM Problems & Solutions

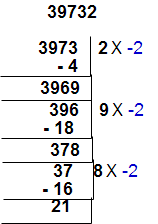
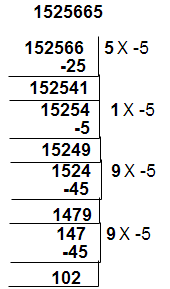







4 thoughts on “Divisibility Rules of numbers from 1 to 20 | Basic math education”
Shortcuts methods of Division math | Tips and tricks for math division
(January 31, 2018 - 12:32 pm)[…] Divisibility Rules for easy calculations of mathematics. […]
WORST SITE EVER
(October 28, 2018 - 5:56 pm)Piece of writing writing is also a fun, if you know afterward you can write otherwise it is complex to write.
Afsha
(June 19, 2019 - 6:23 pm)Great job
sivaalluri
(July 6, 2019 - 5:00 pm)Thank you