Formulas with examples for Sum of n Consecutive numbers
Sum of natural, odd & even numbers
Sum of “n” natural numbers =
Sum of “n” natural even numbers = (n ) (n + 1)
Sum of “n” natural odd numbers = n 2
![Sum of square of "n" first or consecutive square natural numbers | Sum of n Consecutive numbers](https://www.allmathtricks.com/wp-content/uploads/2017/11/Sum-of-square-of-n-first-or-consecutive-square-natural-numbers-1-1.png "Sum of square of \\"n\\" first or consecutive square natural numbers")
![Sum of square of "n" first or consecutive odd numbers | Sum of n Consecutive numbers](https://www.allmathtricks.com/wp-content/uploads/2017/11/Sum-of-square-of-n-first-or-consecutive-square-odd-numbers-1-1.png "Sum of square of \\"n\\" first or consecutive square odd numbers")
![Sum of square of "n" first or consecutive square even number | Sum of n Consecutive numbers](https://www.allmathtricks.com/wp-content/uploads/2017/11/Sum-of-square-of-n-first-or-consecutive-square-natural-even-numbers-.png "Sum of square of \\"n\\" first or consecutive square natural even numbers")
Sum of cube natural, odd & even numbers
Sum of cube of first or consecutive ” n” natural numbers:
![Sum of square of "n" first or consecutive square even number | Sum of n Consecutive numbers](https://www.allmathtricks.com/wp-content/uploads/2017/11/Sum-of-square-of-n-first-or-consecutive-square-natural-numbers-1-3.png "Sum of square of \\"n\\" first or consecutive square natural numbers")
Examples on sum of numbers
Ex . 1 : Find the sum of the first 50 positive integers.
Sol: 1 + 2 + 3+ 4+ 5+ ———-+50 So Here n = 50
= 50 ( 50+1) / 2 = 25 x 51 = 1275
Ex . 2 : Find the sum of the consecutive numbers 25+26+27+28+ —–+100 .
Sol: 25+26+27+28+ —–+50 = ( 1+2+3+4+———+100) – (1+2+3+4+——-24)
= [ 100 ( 100+1) / 2 ] – [ 24 ( 24+1) / 2 ]
= 5050 – 300 = 4750.
Ex . 3 : Find the sum of the squares of the first 60 natural numbers.
Sol: 12 + 22 + 32 + 42+ 52 + ———-+602 So Here n = 60
= { 60 x (60 + 1) x [( 2 x 60 )+1 ] } / 6
= 60 x 61 x 121 / 6
=73810
Ex . 4 : what is the sum of first 100 odd numbers?
Sol : first 100 odd numbers means 1 + 3 + 5 +7 + ———-+ 199 so here n = 100
= 1002 = 10000
Ex . 5 : Find the sum of consecutive odd numbers 51 +53 +55 + ———+ 199.
Sol : 51 +53 +55 + ———+ 199 = {1 + 2+ 3 ———+ 199} – { 1 +2 + 3 + ———+ 49}
=1002 – 252
= 10000- 625 = 9375 .
Ex . 6 : Find the sum of the cubes of the first 25 positive integers.
Sol: 13 + 23+ 33+ 43+ 53 + ———-+253 So Here n = 25
= 252 x (25 +1 )2 / 4
= 625 x 676 / 4 = 105625
Ex . 6 : Find the sum of the cubes of the first 25 odd numbers.
Sol: First 25 odd cube numbers means 13 + 33+ 53 + ———-+493 So Here n = 25
= 25 2 [ (2 x 252 )– 1 ]
= 625 x [ 1250 – 1]
=625 x 1249 = 780625
Ex . 7 : Find the sum of the consecutive cube numbers 263+283+ 303 + 323—–+1003 .
Sol : 263+283+ 303 + 323—–+1003 = {23+43+ 63 + 83—–+1003 } – {23+43+ 63 + 83—–+243}
=(2 x 502 )(50 + 1)2 – (2 x 122 )(12 + 1)2
= [ 5000 x 2601] – [ 288 x 169 ]
= 13005000 – 48672 = 12956328.
Ex . 8 : Find the sum of the consecutive square odd numbers 752 + 772 + 792 + 812+ 832 + ———-+992 .
Sol : 752 + 772 + 792 + 812+ 832 + ———-+992 = {12 + 22 + 32+—–+992 } – { 12 + 22 + 32 + —–+732}
= [ ( 50 ) (4*50 2 – 1) / 3 ] – [ ( 37 ) (4*37 2 – 1) / 3 ]
= [ 50 x 9999 / 3 ] – [ 37 x 5475 / 3]
= 166650 – 67525 = 99125
Some related Topics in Quantitative aptitude
The Concepts of number system the mathematics
Divisibility Rules of numbers from 1 to 20 | Basic math education
Simple interest and Compound interest formulas with examples
Percentage formulas | percentage calculations with examples
Circle formulas in math | Area, Circumference, Sector, Chord, Arc of Circle
Types of Quadrilateral | Quadrilateral formula for area and perimeter
Types of Triangles With examples | Properties of Triangle
Hi friends Thanks for reading. I Hope you liked it. Give feed back, suggestions, comments and please don’t forget to share it
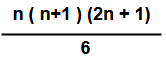
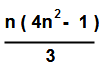
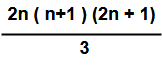
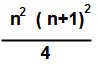
7 thoughts on “Sum of n Consecutive numbers Like Natural, Even, Odd, Squares, Cubes”
Sai Venkatesh malakala
(July 8, 2018 - 8:20 am)Thanks a lot
sivaalluri
(July 9, 2018 - 2:09 pm)Thank you Mr.Sai Venkatesh malakala
Bharathi
(April 9, 2019 - 2:06 am)Thank you sir, please provide more short cut tricks for competitive exams
sivaalluri
(April 20, 2019 - 3:15 pm)Definitely we will upload one by one
Ravindra Nath Mahto
(May 11, 2019 - 5:33 am)Thank you so much sir…
sivaalluri
(May 11, 2019 - 3:43 pm)Thank you
Vijay
(April 16, 2023 - 8:08 am)Thanks for the short trick, need your help to solve below question.
Sum of cubes of six consecutive numbers is 15471. Find the sum of cubes of odd numbers and square of even numbers.