Circle formulas in math | Area, Circumference, Sector, Chord, Arc of Circle

Properties of  circle in math |  Arc, Perimeter, Segment of circle

A circle can be defined as, it is the locus of all points equidistant from a central point. In this we discuss about Properties of circle, circle formulas like area, perimeter, arc length, segment length, segment area... etc.

Terminology related to circles in math:

Origin : It is a center(equidistant) point of the circle. Here “O” is the origin of the circle.

Radius :  Distance from center of circle to any point around it circumference is called Radius of the circle. Generally it is denoted by ” r “.

Diameter: The longest distance from one end of a circle to the other end of the circle is called dia of the circle. Generally it is denoted by ” D ” . Diameter of the circle = 2 x Radius of the circle. i. e  D = 2r.

Arc of a circle: It is a part of the circumference of the circle. The bigger one is called the major arc and the smaller one the minor arc.

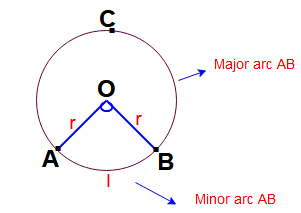Sector of a circle: It is a part of the area of a circle between two radii (a circle wedge).

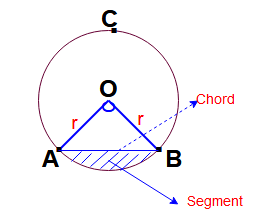
Chord : A line segment within a circle that touches two points on the circle is called chord of a circle.

Circumference : The distance around the circle is called circumference or perimeter of the circle.

Pi ( π ): It is a number equal to  3.141592…  or 22/7.

The pi ( π ) =  (The circumference) / (The diameter) of any circle.

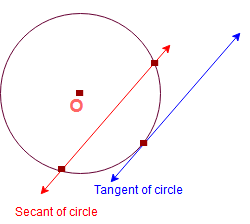
Tangent of circle: a line perpendicular to the radius that touches ONLY one point on the circle.

Secant of circle : A line that intersects a circle at two points then it is called Secant of circle.

Properties of circle :

1. Congruency: Two circles can be congruent if and only if they have equal radii.
2. The perpendicular from the center of a circle to a chord bisects the chord. The converse is also true.
3. The perpendicular bisectors of two chords of a circle intersect at its center.
4. There can be one and only one circle passing through three or more non -collinear points.
5. If two circles intersect in two points then the line through the centers is the perpendicular bisectors of the common chord.
6. If two chords of a circle are equal, then the center of the circle lies on the angle bisector of the two chords.
7. Equal chords of a circle or congruent circles are equidistant from the center.
8. Equidistant chords from the center of a circle are equal to each other in terms of their length.
9. The degree measure of an arc of a circle is twice the angle subtended by it at any point on the alternate segment of the circle.
10. Equal chords of a circle ( or of congruent circles) subtended equal angles at the center.(at the corresponding centers) The converse is also true.
11. If the sum of the opposite angles of a quadrilateral is 180°, then the quadrilateral is cyclic.
12. Secant means a line that intersects a circle at two points. Tangent means it is a line that touches a circle at exactly one point.
13. In two concentric circles , the chord of the larger circle that is tangent to the smaller circle is bisected at the point of contact.

Circle Formulas in Math :

Area and circumference of a circle:

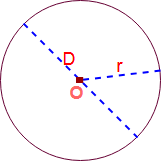Here Origin of the circle = O , Diameter = D and Radius = r

Area of a circle (A ) = π r ² =( π/4 ) D² = 0.7854 D²
Circumference of a circle ( C ) = 2 π r = π D.

Area of circle =( 1/2) x Circumference x radius

A = (1/2) x C x  r

Diameter of a circle (D) = √(A/0.7854).

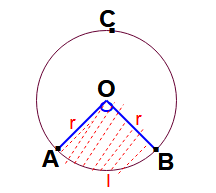
Arc and sector of a circle:

Here angle between two radii is ” θ” in degrees. . And sector of a circle AOB.
Arc length  of circle( l ) (minor) =  ( θ /360) x 2 π r = θ π r / 180

Area of the sector (minor) = ( θ /360) x π r ²

If the angle θ is in radians, then

The area of the sector = (θ/2) r ²

Sector angle of a circle θ = (180 x  l )/ (π r ).

Segment of circle and perimeter of segment:

Here radius of circle = r , angle between two radii is ” θ” in degrees.

Area of the segment of circle = Area of the sector – Area of ΔOAB.

Area of the segment = ( θ /360) x π r ²   –  ( 1 /2) x  sinθ  x r ²

Perimeter of the segment = (θ π r / 180) + 2r sin (θ/2).

Chord length of the circle =  2  √ [ h (2r – h ) ] = 2r sin (θ/2).

Arc  Length of the circle segment   =  l  = 0.01745 x r x θ

Online calculator for circle segment area calculation

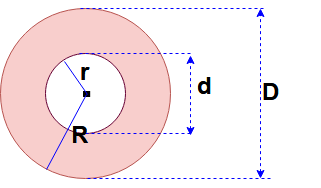
Area of the circular ring:

Here big circle radius = R and Dia = D,

Small circle radius = r and Dia = d,

Area of a circular ring  = 0.7854 (D ² – d ²) = (π/4)  ( D ² – d ²)

Area of a circular ring  = π (R ² – r ² ).

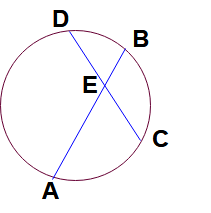
Formula for intersecting chords in circle:

Here AB and CD are two chords in circle and intersecting each at the point E.

Then AE : EB = DE : EC.

 

 

 

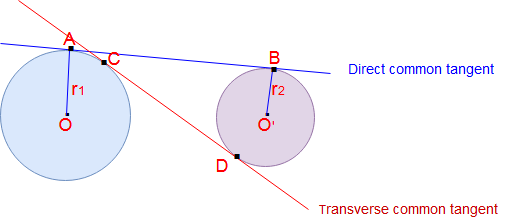
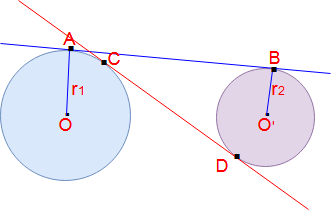
Formula for length of the tangents of circles:

Here Two circles origins O & O’  and radius are r1 and r2 respectively.

Direct common tangent  AB &  transverse common tangent = CD

Length of  direct common tangent AB = √ [ (Distance between two origins)² – (r1 -r2)² ]

= √ [ (OO’)² – (r1 -r2)² ]

Length of transverse common tangent AB = √ [ (Distance between two origins)² – (r1 +r2)² ]

= √ [ (OO’)² – (r1 +r2)² ]

Geometry Math

Two dimensional shapes formulas.

Quadrilateral Properties | Trapezium, parallelogram, Rhombus

Types of Triangles With examples | Properties of  Triangle

Number System.

Number Categories

Rules for Divisibility of numbers

Formulas for Sum of n Consecutive numbers

Methods to find HCF & LCM

GCD and LCM Problems & Solutions

Hi friends Thanks for reading. I Hope you liked it. Give feed back, comments and please don’t forget to share it.