Classifications of Triangles with properties | Triangle Area Formulas

Types of Triangles With examples | Properties of  Triangle

A simple closed figure bounded by three lines segments is called triangle.

The triangle can be defined as  “A two dimensional plane figure with three straight sides and three angles”.

Terminology and Formulas of the Triangles:

Triangle Sides :

The three lines segments that form the triangle area called sides of triangle. AB = c, BC = a, CA = b are the sides of the ΔABC ( triangle ABC). The Sum of any two sides of a triangle is always greater than the third side.

i.e  a + b  > c , b + c > a ,  c + a > b

Vertex :

Two adjacent sides of a triangle intersect at a point. That point is called vertex. The points A, B, &C area called vertices or angular of ΔABC ( triangle ABC) .

Angle :

Two lines segments with the same end point will determine one angle. Triangle has 3 angles namely

∠ABC, ∠BCA, ∠CAB and they also denoted as ∠B, ∠C, ∠A respectively. Always the sum of the angles of a triangle is $180°$

i.e ∟A + ∟B + ∟C = $180°$

Perimeter of a Triangle :

The sum of the measures of the three sides of the a triangle is called the perimeter of the triangle. The sum of the sides AB = c , BC = a  & CA= b is equal to perimeter of  ΔABC ( triangle ABC).

i.e perimeter of  ΔABC =  AB + BC + CA = a +b + c

Triangular Area or Region :

The interior of a triangle together with its boundary is called the triangular region or triangular area.

Area of the triangle = (1/2) x Base x Height

Area of the triangle ABC = (1/2) x  a x h

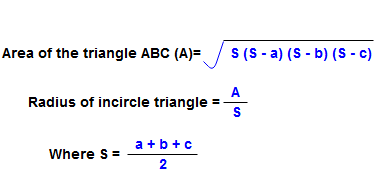
Median of the triangle :

The line joining the midpoint of a side of a triangle to the positive vertex is called the median of the triangle. Here AR, BQ, CP are the medians of the triangle ΔABC. The median of a triangle divides the triangle into two triangles with equal areas.

i.e Area of the ΔARB = Area of the ΔARC

Area of the ΔBQA= Area of the ΔBQC

Area of the ΔCPB = Area of the ΔCPA

Triangle centroid:

The point where the three medians of a triangle meet is called centroid of that triangle. The point  ” s” is the centroid of the triangle ΔABC. The triangle centroid divides each the median of the triangle into the  $2:1$ratio segments.

i.e As : sR = 2 : 1

Bs : sQ = 2 : 1

Cs : sP = 2 : 1

Area of a triangle formed by joining the midpoints of the sides of a given triangle is one-fourth of the area of the given triangle.

Area of the triangle ABC = 1/4 area of the triangle PQR  ( area of ΔABC = 0.25 x area of  ΔPQR )

Classification of the triangles:

Triangles can be classified into three kinds according to measures of their sides and three kinds according to the measures of angles.

$Classification\; according\; to\; sides:$

According to the sides the triangles classified as Equilateral, isosceles and Scalene

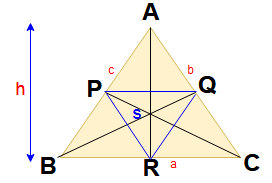
Equilateral triangles :

A triangle having all the three sides of the same length is called an equilateral triangle. All three  angles of equilateral triangles are equal.

 

i.e   PQ = QR = RP =  a

∠P, ∠Q, ∠R = 60°

Formulas for equilateral triangle :

Perimeter of the equilateral triangle = 3 a

Area of the equilateral triangle = (√3/4) x a²

Radius of incircle of an equilateral triangle =  a / (2 √3)

Radius of circumference circle of an equilateral triangle =   a / √3

Isosceles Triangles :

A triangle having two sides of equal length is called an isosceles triangle. The angle opposite to the equal sides of an isosceles triangle area equal.

Here  PQ = PR  = a and ∠Q = ∠R

Scalene Triangles :

If the three sides of a triangle are of different length then the triangle is called scalene triangle.

If  PQ ≠ QR ≠ R or ∠P ≠ ∠Q ≠ ∠R then ΔPQR  is called scalene triangle.

$Classification\; according\; to\; angle:$

According to their angles divided three kinds of triangles. They are acute angled triangle, Right angled triangle and obtuse angled triangle

Acute Triangle :

All angles of this triangles area having less than 90°. So all equilateral triangles area acute triangles.

If ∠P < 90° ,  ∠Q  < 90° & ∠R < 90° than ΔPQR  is called Acute triangle.

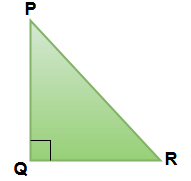
Right Triangle :

If triangle having one 90° angle  than it is called right angled triangle.

If triangle having a right angle (i.e 90°) and also two equal angles ( i.e 45° & 45° ) then it is called  Right Isosceles Triangle

Here ∠Q  = 90° So ΔPQR  is called right angle triangle.

If  ∠P = ∠R = 45°  then ΔPQR  is called Right Isosceles Triangle.

Obtuse Triangle :

If triangle having one more than 90° angle  than it is called Obtuse angled triangle.

Here ∠P  > 90° So ΔPQR  is called Obtuse angled triangle.

Properties of the Triangles:

1. The sum of the three angles of the a triangle is two right angles (i.e 180° ).
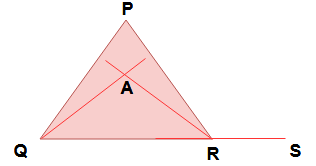
2. If one sides of the triangle is produced , the exterior angle formed is equal to the sum of the interior opposite angles. Here ∠P = ∠Q = ∠PRS.
3. The internal bisectors of  ∠Q and ∠R of  ΔPQR intersect at A. Then ∠A = 180° + (∠P / 2 )                                          ( Note : Bisectors means ∠AQP = ∠AQR and ∠ARP = ∠ARQ )
4. If any two angles and a sides of one triangle are equal to two angles and the corresponding side of the other triangle, then the two triangles are congruent.
5. If two medians of triangle are equal then the triangle must be an Isosceles triangles.

Geometry Math

Two dimensional shapes formulas.

Properties of  circle in math |  Arc, Perimeter, Segment of circle

Quadrilateral Properties | Trapezium, parallelogram, Rhombus

Topics in Quantitative aptitude math for all types of exams

Hi friends Thanks for reading. I Hope you liked it. Give feed back, comments and please don’t forget to share it.