Centroid of the triangle meaning,defination,properties, formula & examples

In this article, we will learn about the centroid of the triangle formula with derivation and also given some examples with solutions.

In coordinate geometry, the centroid of the triangle is used frequently to measure a point of coincidence of the median or mid of the triangle. The median or mid of the triangle is the point where all the points meet after dividing the triangle into smaller parts. The median of the triangle cuts the triangle into two smaller triangles and go through mid of the triangle.

Table of Contents

What is the centroid of a triangle?

The centroid of the triangle is formed by cutting the triangle three times and making three medians on it. The central point where all the three medians intersect is known as the centroid of the triangle. A Median is formed when each vertex of the triangle meets the opposite vertex of the triangle.

Where all the points of median intersect from the centroid of the triangle is also known as the point of concurrency. Each median has points from initial to final travel in a triangle. These points of medians are used to calculate the centroid of the triangle.

Properties of the centroid of the triangle

1) The geometric center of an object can also be used in place of the centroid.

2) Centroid always occurs inside the triangle because each vertex draws a median inside the triangle to the opposite vertex.

3) Centroid is at 2/3 distance from the vertex to the midpoint and divides the median in ratio 2:1.

4) Centroid is that point that occurs by taking the midpoint of all the three medians.

5) To calculate the length of the median segment, distance from the centroid from the vertex of the triangle can be used.

Formula to find the coordinates for centroid of the triangle

The centroid of a triangle is the point of intersection of its medians. To find the coordinates of the centroid of a triangle required coordinates of the vertices of the triangle.

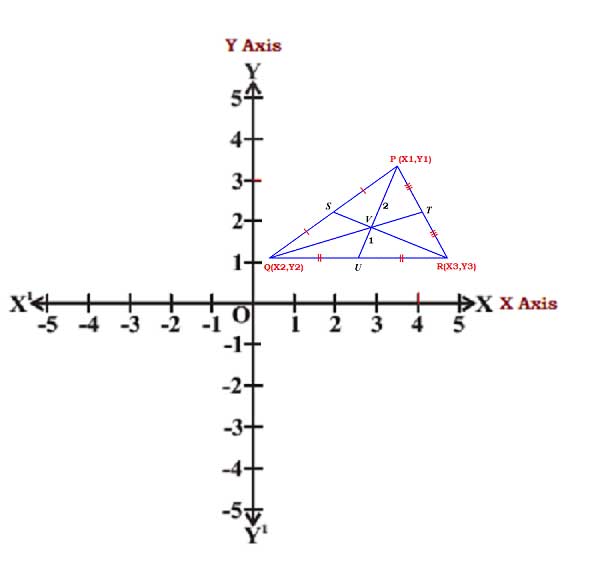
In the above P(x1, y1), Q(x2, y2) and R(x3, y3) be the vertices of the triangle △PQR. Here PU be the median bisecting its base of QR.

So the center point of the base QR is U. Coordinates of the center point of the “U”

$U = \left[ \frac{X_{2} + X_{3}}{2} \ , \frac{Y_{2} + Y_{3}}{2} \right]$

Now the point V on PU which divides it internally in the ratio 2 : 1, is the centroid and we already know the coordinates of the P & U

Let (x, y) be the coordinates of V, and then we use the section formula to find the coordinates of the centroid of V

$V(x, \ y) = \left[ \frac{2\left( \frac{X_{2} + X_{3}}{2} \right) + 1(X_{1})}{2 + 1}, \ \frac{2\left( \frac{Y_{2} + Y_{3}}{2} \right) + 1(Y_{1})}{2 + 1} \right]$

$V(x, \ y) = \left[ \frac{X_{1} + X_{2} + X_{3}}{3}, \ \ \frac{Y_{1} + Y_{2} + Y_{3}}{3} \right]$

Hence, the coordinates of the centroid of the triangle are given below

$\text{Centroid of the triangle} = \left[ \frac{X_{1} + X_{2} + X_{3}}{3}, \ \ \frac{Y_{1} + Y_{2} + Y_{3}}{3} \right]$

Let us see some examples of finding the coordinates for the centroid of the triangle

Example 1 : Find the centroid of a triangle by using given vertices, (12, 34), (13, 23), and (2, 3)?

Solution

Step 1: Take the given vertices and give a name to each point.

(12, 34), (13, 23), (2, 3)

x₁ = 12, y₁ = 34

x₂ = 13, y₂ = 23

x₃ = 2, y₃ = 3

Step 2: Now take the general formula to calculate

$\text{Centroid of the triangle} = \left[ \frac{X_{1} + X_{2} + X_{3}}{3}, \ \ \frac{Y_{1} + Y_{2} + Y_{3}}{3} \right]$

Step 3: Put the values of vertices in the above formula.

= [(12 + 13+ 2)/3, (34 + 23 + 3)/3]

= (27/3, 60/3)

= (9, 20)

Hence, the centroid is (9, 20) by using given vertices.

Example 2 : Find the centroid of a triangle by using given vertices, (21, 41), (-3, -13), and (-12, -17) ?

Solution

Step 1: Take the given vertices and give a name to each point.

(21, 41), (-3, -13), (-12, -17)

x₁ = 21, y₁ = 41

x₂ = -3, y₂ = -13

x₃ = -12, y₃ = -17

Step 2: Now take the general formula to calculate

$\text{Centroid of the triangle} = \left[ \frac{X_{1} + X_{2} + X_{3}}{3}, \ \ \frac{Y_{1} + Y_{2} + Y_{3}}{3} \right]$

Step 3: Put the values of vertices in the above formula.

= [ (21 + (-3) + (-12)/3, 41 + (-13) + (-17)/3]

= [ (21 – 3 – 12)/3, (41 – 13 – 17)/3]

=[ (21 – 15)/3, (41 – 30)/3]

= (6/3, 11/3)

= (2, 11/3)

Hence, the centroid is (2, 11/3) by using given vertices.

Example 3 : Find the centroid of a triangle by using given vertices, (-2, -4), (13, 43), and (31, 17)?

Solution

Step 1: Take the given vertices and give a name to each point.

(-2, -4), (13, 43), (31, 17)

x₁ = -2, y₁ = -4

x₂ = 13, y₂ = 43

x₃ = 31, y₃ = 17

Step 2: Now take the general formula to calculate

Centroid of the triangle = (x₁ + x₂ + x₃/3, y₁ + y₂ + y₃/3)

Step 3: Put the values of vertices in the above formula.

=[ (-2 + 13 + 31)/3, (-4 + 43 + 17)/3]

= [(-2 + 44)/3, (-4 + 60)/3]

= (14, 56/3)

Hence, the centroid is (14, 56/3) by using given vertices.

Example 4 : Find the centroid of a triangle by using given vertices, (12, 4), (-33, 3), and (-1, -7)?

Solution

Step 1: Take the given vertices and give a name to each point.

(12, 4), (-33, 3), (-1, -7)

x₁ = 12, y₁ = 4

x₂ = -33, y₂ = 3

x₃ = -1, y₃ = -7

Step 2: Now take the general formula to calculate

Centroid of the triangle = (x₁ + x₂ + x₃/3, y₁ + y₂ + y₃/3)

Step 3: Put the values of vertices in the above formula.

= (12 + (-33) + (-1)/3, 4 + 3 + (-7)/3)

= (12 – 33 – 1/3, 4 + 3 – 7/3)

= (12 – 34/3, 7 – 7/3)

= (-22/3, 0/3)

= (-22/3, 0)

Hence, the centroid is (-22/3, 0) by using the given vertices.

Some more examples for practice

Example: 5 – Find the centroid of the triangle whose vertices are (3, −5), (−7, 4), (10, −2)
respectively.

Answer: centroid is (2, −1)

Example: 6 – Find the centroid of the triangle whose vertices are (−4, 6), (2, −2) and (2, 5) respectively.

Answer: centroid is (0, 3)

Online Calculator

An online centroid of a triangle calculator can also be used for finding of centroid by given vertices to avoid lengthy calculations and get results in a couple of seconds.

Related articles:

Coordinate geometry introduction | cartesian plane, quadrants, X-coordinate, Y-coordinate

Types of Lines | Straight and Curved Line | Lines In Geometry

Transversal Angles | Angles formed by parallel lines and transversal Line

Lines in Geometry | line segment math definition | Ray along with their types

Point in Geometry Math | Collinear Points and non-collinear points Examples

Complementary and supplementary angles | Types of Angle Pairs

Angles in Math | Acute, Right, Obtuse, Straight, Reflex & Complete angle

Formulas of area and perimeter for Triangle, Trapezium, parallelogram, Rhombus, Rectangle, Square, kite, circle, Ellipse

Quadrilateral formula for area and perimeter

Formulas for Arc, Perimeter, Segment of circle