The abbreviation of cubic feet is “ft³,” which is the unit of volume used in different fields like construction, engineering, and everyday measurements. This unit is used to find the amount of quantifying of those spaces given in three-dimensional objects.
In this article, we will discuss the definition and formula of cubic feet, different conversion units of cubic feet, and calculating methods of cubic feet. In addition, with the help of detailed examples and their solution.
Definition of Cubic Feet
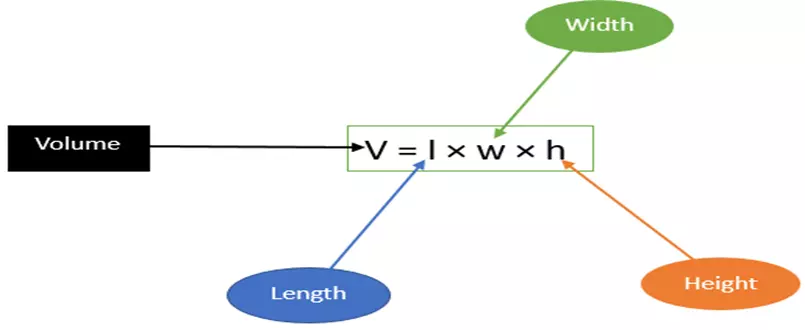
Cubic feet measure the volume of a three-dimensional space and are derived from the multiplication of length, width, and height.
The formula of cubic feet to determine the volume (V) is:
Cubic Feet (ft3) = Length (ft) × Width (ft) × Height (ft)
Cubic Feet (ft3) = L (ft) × W (ft) × H (ft)
Cubic Feet Conversion
Cubic Inches to Cubic Feets:
First we convert the length, width, and height are into feet from inches. Hence from Inches we need to divide each value by 12.
Then we use the volume formula of Cubic Feet (ft3) = Length (ft) × Width (ft) × Height (ft)
For direct conversion from cubic inches to cubic foot required to divide the volume by 1728 cubic inches (because it’s 123 ). So, the simple formula is used for the conversion of cubic inches into cubic feet.
Cubic Feet = Cubic Inches ÷ 1728
Now, we explain this concept with the help of a practical example so, let’s suppose the volume is 3456 cubic inches, then according to the formula cubic feet would be (3456 in³ ÷ 1728 = 2ft³).
Cubic Yards to Cubic Feets:
First we convert the length, width, and height are into feet from yard. Hence from yard we need to multiply each value by 3.
Then we use the volume formula of Cubic Feet (ft3) = Length (ft) × Width (ft) × Height (ft)
For direct conversion from cubic yard to cubic foot required to multiply the volume by 27 cubic yards (because it’s 33 ).
So, the simple formula is used for the conversion of cubic yard into cubic feet.
Cubic Feet = Cubic yard x 27
Cubic Centimeters to Cubic Feets:
First we convert the length, width, and height are into feet from Centimeters.
Hence from centimeters we need to divide each value by 30.48. After we can use volume formula of Cubic Feet (ft3)
For direct conversion from cubic centimeters to cubic foot required to divide the volume by 28,316.847 cubic centimeters (because it’s 30.48 3 ).
So, the simple formula is used for the conversion of cubic centimeters into cubic feet.
Cubic Feet = Cubic centimeter ÷ 28316.847
Cubic meters to Cubic Feets:
First we convert the length, width, and height are into feet from meters. Hence from yard we need to multiply each value by 3.281.
Then we use the volume formula of Cubic Feet (ft3) = Length (ft) × Width (ft) × Height (ft)
For direct conversion from cubic meters to cubic feet required to multiply the volume by 35.315 cubic meters (because it’s 3.2813 ).
So, the simple formula is used for the conversion of cubic yard into cubic feet.
Cubic Feet = Cubic meters x 35.315
Cubic Feet to Liters: 1 cubic feet is approximately equal to 28.3168 liters. Hence for conversion from cubic feed to liters use this factor of 28.3168.
Cubic Feet to Gallons: 1 cubic foot is approximately equal to 7.48052 gallons. Hence for conversion from cubic feed to gallon use this factor of 7.48052.
Calculation of Volume in Cubic Feet
Understanding how to perform calculations involving cubic feet is essential for various applications, from estimating material quantities in construction to determining storage capacities. To find volume in cubic feet by using above conversion factors.
Volume of Irregular Shapes
For irregular shapes, the volume can be calculated by dividing the object into smaller, more manageable shapes and summing their volumes.
V (total) = V1 + V2 +…+ Vn
If an irregular shape is given and the target is to determine the volume of an irregular shape, we follow the following method to determine the volume of a given irregular shape.
- Visualize the Irregular Shape
- Divide into Manageable Sections
- Measure or Estimate Dimensions
- Use Appropriate Volume Formula
- Sum the Individual Volumes
- Consider Unit Consistency
- Account for Gaps or Hollow Spaces
- Verify Results and Units
- Document the Process
Cubical Storage Space
When determining storage space requirements, you can calculate the volume of the available space and compare it with the volume of the items you need to store.
Unused Space = Total Space – Occupied Space
If you have a storage room with dimensions of 8 feet by 6 feet by 10 feet (480 cubic feet) and your items occupied 200 cubic feet, the unused space would be 480, ft³ – 200, ft³ = 280 ft³.
Example 1:
Determine the measurement of a room, and the side of the room length, width, and height are given by Length=12ft , width=25ft, and height = 50ft
Solution:
Given side data of room is L= 12ft W=25 ft, and H = 50ft
The formula used to find the cubic feet
Cubic Feet = L × W × H
Now, we put the value in our given formula we get our required result.
Cubic Feet = 12 × 25 × 50
Cubic Feet = 15000 ft3
Example 2:
Determine the measurement volume of the freeze in liters as per the following diagram.
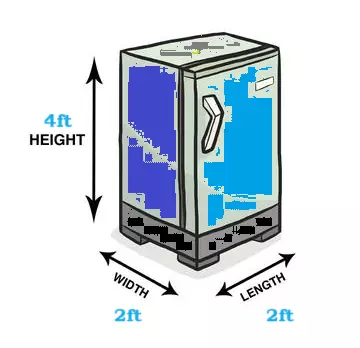
Solution:
Given side data of room is L= 2ft W=2ft, and H = 4ft
The formula used to find the cubic feet
Cubic Feet = L × W × H
Now, we put the value in our given formula we get our required result.
Cubic Feet = 2 x 2 x 4 = 16 ft3
1 cubic feet is approximately equal to 28.3168 liters
Volume of freeze = 16 x 28.3168 = 453 liters.
Example 3:
Find the volume of the irregular-shaped box and the side value of the box in length is 200 yards, width is 150 yards, and height of the irregular-shaped box is 5 ft.
Solution:
Our given data of irregular box is length = 200 yards, width = 150 yards And, Height = 15ft
Convert all values in feet, because in the formula of cubic feet, we use all values in unit feet. So,
L = 200yard= 200*3 = 600 feet
W = 150 yards *30 = 450 feet
and Height = 15ft
By using the formula of volume of cubic feet.
Cubic Feet = 600 × 450 × 15
Cubic Feet= 4050000 ft3
Example 4:
Find the volume of a 20-foot container measures 5.90 meters in length, 2.35 meters in width and 2.39 meters in height.
Solution:

Our given data of container is length = 5.9m , width = 2.35m and, Height = 2.39m
Convert all values in feet, because in the formula of cubic feet, we use all values in unit feet. So,
L = 5.90 *3.281 = 19.36 feet
W = 2.35*3.281 = 7.71 feet
and Height = 2.39*3.281 = 7.84 feet
By using the formula of volume of cubic feet.
Cubic Feet = 19.36*7.71*7.84
Cubic Feet= 1170.2 ft3
Summary
The article comprehensively covers the definition, formula, conversion units, and practical applications of cubic feet. Detailed examples enhance understanding, enabling readers to confidently discuss and apply the concepts presented.
Frequently asked question
Question number 1:
What are the common uses of cubic feet?
Answer:
Cubic feet are widely used in construction to quantify the volume of materials, in shipping and storage to determine capacities, and in various industries for measuring and analyzing three-dimensional spaces.
Question number 2:
What is the significance of cubic feet in real estate?
Answer:
Cubic feet are often used in real estate to determine the volume of rooms, buildings, or storage spaces. This information is valuable for assessing space utilization and planning interior layouts.
Question number 3:
Can you convert cubic feet to liters?
Answer:
Yes, cubic feet can be converted to liters. The conversion factor is approximately 28.3168 liters per cubic foot. To find the volume in liters multiply the volume in cubic feet.
Related Articles:
Basic Concepts of Coordinate geometry
Volume of cube and cuboid, Area of cube and cuboid
Frustum of cone formulas with examples | Surface area and Volume
Surface Area and Volume of a Prism Formula
Surface Area and Volume of a Cone formula
Volume and Surface Area of a Cylinder Formulas
Surface Area and Volume of Sphere, Hemisphere, Hollow Sphere Formulas
Properties of circle in math | Arc, Perimeter, Segment of circle






