Volume and surface area of a cone formulas | Cone Defination, Application

Definition of Cone

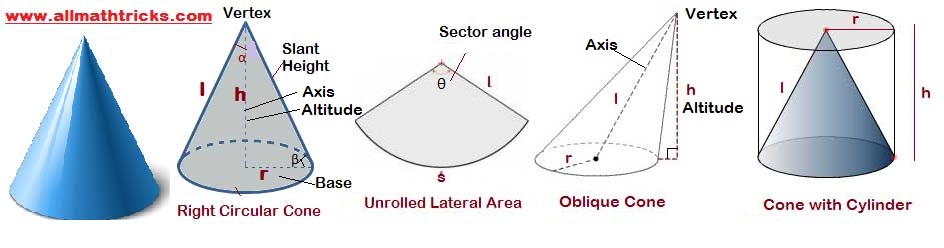
A cone is a three-dimensional shape in geometry. The object have curved (lateral) surface with a vertex and a circular base is called circular cone.

i. e A cone is a solid which has a circular at its base and a slanting lateral surface that converges at the apex.

Its dimensions are defined by radius of the base ( r), the height ( h) and the slant height ( l).

Height of a cone ( h)– the distance from the vertex of the cone to the base

Radius of a cone (r) – The circular base has measured value of radius

Slant height of a cone ( l) – The length of the cone from the any point on the circumference of the base to vertex of the cone

Difference between Right circular cone & Oblique cone.

The axis of the cone is the segment whose endpoints are center of the base to vertex or apex. If the axis of the cone is perpendicular to the plane of the circle, then it is called as a right circular cone otherwise it is an oblique cone.

Formulas of Right Circular Cone

Curved or lateral surface area of the cone = (1/2) x Slant height x length of the entire curved boundary.

Here length of the entire curved boundary = Circumference of the base of the cone = 2 π r

Lateral surface area(LSA) of cone = $\frac{1}{2} \times l \ \times 2\pi \ r$ = π r l

LSA of cone = π r l

Note: Slant height = l = $\sqrt{r^2 + h^2}$

Total surface area (TSA) of the cone = Lateral surface area of cone + Base area of the cone = π r l + π r ²

TSA of cone = π r ( l + r)

Volume of the cone is one-third the volume of the cylinder with same base radius.

Volume of a cone = $\frac{1}{3} \pi r^2 h$

Opening angle = Sector angle = ( θ) = 2 x arc sin( r / l )

Base Angle β = ( 180° – α ) / 2

r = h tan(α) = l sin(α)

Formulas of Volume of an Oblique Cone

For an oblique cone, slant height is undefined so there are no formulas for the areas of oblique cones.

The volume of a oblique cone is same as right circular cone.

i.e The volume of oblique cone is one-third the product of altitude and area of its base.

Volume of an Oblique Cone = $\frac{1}{3} \pi r^2 h$

Application on cone formulas

Example-1 : Find curved surface area of a right circular cone of height 15 cm and base diameter is 16 cm

Solution:

Curved surface area of a right circular cone = π r l = π D l /2

Slant height = l = $\sqrt{r^2 + h^2}$ = $\sqrt{8^2 + 15^2}$ = 17

= π x (16/2) x 17 = 136 π cm²

Example – 2: The radius of base of a right circular cone is 7 cm and its slant height is 25 cm. Find the volume of cone.

Solution: Volume of cone = $\frac{1}{3} \pi r^2 h$

Altitude of cone = h = $\sqrt{l^2 - r^2}$ = $\sqrt{25^2 - 7^2}$ = 24

Volume of cone = (1/3) x (22/7) x 7 x 7 x 24 = 1232 cm³

Example – 3: Find the volume of the largest right circular cone that can be cut out of a cube whose edge is 9 cm.

Solution: Volume of cone = $\frac{1}{3} \pi r^2 h$

Here radius of cone =r = 9/2 = 4.5 cm

height of a cone = h = 9

Volume of cone = (1/3) x (22/7) x (9/2) x (9/2) x 9 = 190.93 cm³

Example -4 : A Cone is cut parallel to its base in such a way that height of two parts is same. Find the ratio of volume of these two parts.

Solution: Let radius of small cone = r & height = h

Then large cone height = 2h & radius = 2r

Volume of a cone = $\frac{1}{3} \pi r^2 h$

= (1/3) π r² h : (1/3) π (2r)² (2h) = 1 : 8 ( Here total parts is 8)

Ratio of volume of two parts = 1 : 7

Example – 5 : A Cone is cut parallel to its base in such a way that height of three parts is same. Find the ratio of volume of these three parts.

Solution: Let radius of small cone = r & height = h

Then middle cone height = 2h & radius = 2r

Then large cone height = 3h & radius = 3r

Volume of a cone = $\frac{1}{3} \pi r^2 h$

= (1/3) π r² h : (1/3) π (2r)² (2h) : (1/3) π (3r)² (3h) = 1 : 8 : 27 ( Here total parts is 27)

Ratio of volume of three parts of cones= 1 : 7 : 19

Example-6 : A cone is cut parallel to its base in such a way that the volume of the smaller cone is 1/729 times of bigger cone. Find the height of the small cone if the side is cut 48cm above the base.

Solution: Ratio of volumes of smaller cone to bigger cone = 1 : 729 = 1³ : 9³

i.e Height or radius = 1 : 9

Ratio of height for both cones is 1 : 8

Let height of the small cone = a

Then height of the large cone = 8a = 48 cm

a = 6 cm

Height of small cone = 6 cm

Example -7 : The ratio of height and diameter of a right circular cone is 3 : 2 and volume is 1078 cm³, then find its cone height.

Solution: Take the diameter and height of the cone are 2a & 3a respectively

Volume of a cone = $\frac{1}{3} \pi r^2 h$ = 1078 cm³

⇒ ( 1/3) x ( 22/7) x (a)² x (3a)= 1078

⇒ a ³ = 7 ³