Surface Area and Volume of Sphere, Hemisphere, Hollow Sphere Formulas, Examples

In this article provided formulas of Surface Area and Volume of a Sphere and a Hemisphere with examples. Volume and surface area of a three dimensional (3D) solid geometrical shapes.

Sphere and Hemisphere Formulas with Examples

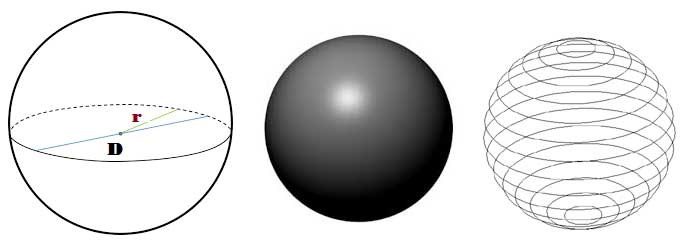
Sphere

Sphere is a one of the three dimensional solid figure, Which made up of all points in the space, Which lie at a constant distance called the radius, from a fixed point called the center of a sphere. ( i.e The set of all points in the three space equidistant from a given points form sphere)

Surface Area of a Sphere

Surface area of the sphere will be covered completely fill the region of four circles, all of the same radius as of the sphere. So

Surface area of a Sphere with radius ( r )  = 4 x ( π r² ) = 4 π r²

Volume of a Sphere

Volume of a sphere is equal to 4 π/3 times the cube of its radius.

Volume of a sphere =

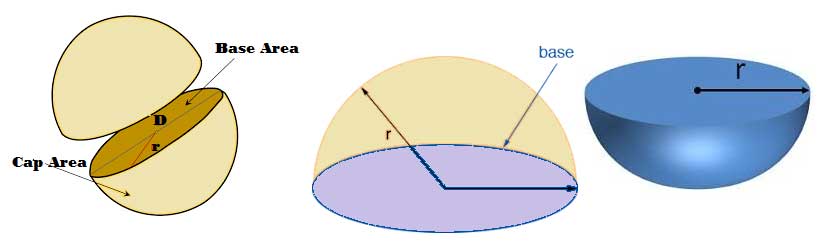
Hemisphere

The solid sphere is divided into two equal parts and its each half part is called a hemisphere.

Surface Area of a Hemisphere

Surface area of the hemisphere having two faces. There is curved face (Cap Area) and flat face ( base area).

Surface area of a Sphere with radius ( r )  = 4 π r²

Then cap area of hemisphere is half surface area of the sphere

i.e Cap Area or Curved surface area of the hemisphere = 1/2 ( 4 π r² ) = 2 π r²

Flat surface area or base area of the hemisphere = Area of the circle with same radius = π r²

Total Surface Area of the Hemisphere = 3 π r²

Volume of a Hemisphere

Hemisphere is half of a sphere

Volume of a hemisphere  = ( 1/2 ) ( 4 /3 π r² ) =

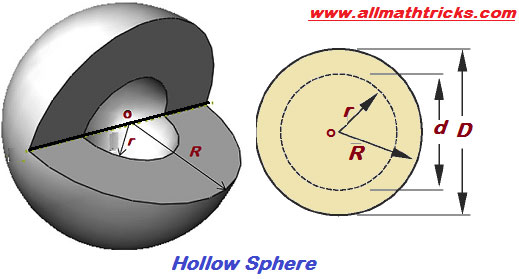
Surface Area and Volume of Hemisphere shell

Take external radius is ‘R’ and inner radius is ‘r’ of hemisphere

then

Curved surface area of hemisphere shell = 2 π  ( R² + r² ) ( Considered inside and outside area of hemisphere)

Volume of Hemisphere shell =

Volume of Hollow Sphere

Here Hollow sphere inner radius – r & outer radius – Rr

Volume of allow sphere =

Solid Sphere

Solid Sphere is the region in space bound by a sphere.

Examples on surface area and volume of sphere and hemisphere

Example -1 : Find the surface area and volume of sphere having the radius 7 mm

Solution: Here radius of sphere  = r = 7 mm

Now Surface area of a Sphere = 4 π r²

= 4 x (22/7) x 7 x 7 = 616 mm²

Volume of a sphere =   = (4312/3 ) mm³

Example-2 : A shot-put is a metallic sphere of radius 2.1 cm and density of the metal used for same is 7.8 gm/cm³. Find the weight of the shot-put

Solution: The shot-put is a solid sphere with the radius 2.1 cm

Volume of shot-put =   = (4/3) x (22/7) x 2.1 x 2.1 x 2.1 = 38.8o8 cm³

Density of metal used for making shot-put is 7.8 gm/cm³

Weight of the shot-put = 38.8o8 x 7.8 ( gm x cm³ /cm³ ) = 302.7 gm

Example-3 : The volume of a solid hemisphere is 18π mm³. Find the total surface of the same.

Solution: Take the radius of sphere = r, then

Volume of a sphere =

⇒   = 18π

⇒ r = 3

Total Surface area of hemisphere = 3 π r² = 27 π

Example-4: The three metallic spheres have radii 3cm, 4cm & 5cm respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.

Solution: Take the radius of final sphere is R

Volume of final sphere = volume of individual spheres

⇒ (4/3) x π x R³ = (4/3) x π x 3³ + (4/3) x π x 4³ + (4/3) x π x 5³

⇒ R³ = ( 3³ + 4³ + 5³ ) = 6³

⇒ R = 6

Example-5 : A hemispherical bowl has a radius of 4.2 cm. What would be the volume of mercury it would contain?

Solution: Here radius of hemispherical bowl = r = 4.2 cm

Volume of a hemisphere  =   = (2/3) x (22/7) x 4.2 x 4.2 x 4.2 = 155.232 cm³

Note: Here asked only volume of mercury. In case of ask mass of the mercury then multiplying with density with volume)

Example-6: A metallic sphere have diameter of 6 cm. The metallic sphere is melted and manufacturing into a wire of uniform cross section. Find the radius of wire if the length of the wire is 36 m.

Solution: Here radius of sphere = r = 3 cm &  Length of wire = 36 m = 3600 cm

Volume of Sphere = Volume of wire

⇒ (4/3) π r³  = π r² h

⇒ ( 4/3)  x ( 22/7) x 3 x 3 x 3   = (22/7) x r² x 3600

⇒ r = 1/10 cm = 1 mm

Example-7: Volumes of two spheres are in the ratio 125:64. Then find the ratio of their surface areas.

Solution: Take radius of spheres are r₁ and r₂

Ratio of volume of Spheres = 125 : 64

⇒   = 125 : 64

⇒ r₁  : r₂ = 5 : 4

Ratio of surface area of spheres

⇒   = r₁ ²: r₂ ² = 5² : 4 ²  = 25 : 16

Example-8: A hemisphere tank is fabricated with an iron sheet of 1 cm thick. If the inner radius is 10 cm , then find the weight of the iron used to make the tank. (To be take Density of iron = 7 gm/cm³)

Solution: Hemisphere inner radius = 9 cm,then outer radius = 10 cm

Volume of shell of hemisphere =

= ( 2/3 )x (22/7) x ( 10³ – 9³) = ( 2/3 )x (22/7) x (1000 – 729) = (11924/21) cm³

Weight of the iron required = (11924/21) x 7 = (11924 /3) = 3974.66 gm

Thanks for reading this article. I Hope you liked this article of “ Surface area and volume of a sphere, Hemisphere and hollow sphere formulas with examples ”. Give feed back and comments please.

Related Articles

Surface Area and volume of cuboid and Cube

Area, Circumference, Sector, Chord, Arc of Circle

Formulas of Rectangle, Square, Trapezium, parallelogram, Rhombus, kite

Formulas & properties of Triangles

Lines, line segment and ray

Interior angles, Exterior Angles, Alternate Interior & Alternate Exterior Angles