How many squares and rectangles are there in this picture | All Math Tricks

In this article discussed about formulas to find number of squares and rectangles in given figure of  of  ‘n’ number of rows and ‘m’ is the number of columns

 Count number of squares and number of rectangles in a given N x M Grid | How to count square in reasoning

How many squares are there in the given figure

How many squares are there in the figure of  same number of rows and columns

( i.e Number of squares in square grid )

Example – 1 :

  How many squares are there in an 4 x 4 grid

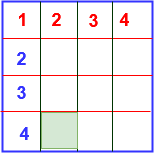
Solution : There are 4 rows and 4 columns in the above figure.  So let n =4

Here we using two types of formulas for finding number of squares in an n x n grid  as follows

Formula – 1

n² + (n -1 )² + (n-2)² + – – – – – + (n – n)²

Now substitute n = 4 in the above formula

= 4² + ( 4-1)²  + (4- 2 )² + (4 – 3)²   + (4 – 4)²

= 16 + 9 + 4 + 1 + 0 = 30

Formula – 2

Apply the formula   
Substitute n = 4 in above formula

= 4 x 5 x 9 / 6 = 30

So number of squares in an 4 x 4 grid is 30

Example -2
How many squares are there in an 5 x 5 grid

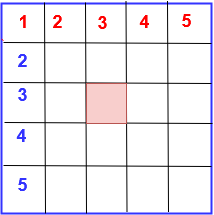
Solution : There are 5 rows and 5 columns in the above figure. Hence n=5

Formula

n² + (n -1 )² + (n-2)² + – – – – – + (n – n)²

So according to above substitute n = 5

= 5² + ( 5-1)² + (5- 2 )² + (5 – 3)² + (5 – 4)²+ (5 – 5)²

= 25 + 16 + 9 + 4 + 1 + 0 = 55

Number of squares in an 5 x 5 grid is 55

How many squares are there in the figure of’n’ number of rows and ‘m’ number of columns

( i.e Number of squares in rectangle grid )

Example – 3 How many squares are there in an 3 x 4 grid

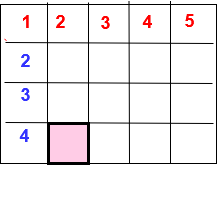
Solution : There are 4 rows and 5 columns in the above figure.

Let number of rows ( n)= 4 & number of columns (m) = 5

Here we using simple formulas as follows

Formula- 1

( n x m ) + (n -1 ) (m – 1)  + (n-2 ) ( m- 2)  + – – – – – + (n – n ) or (m – m)

Now substitute n = 5 and m = 4

= ( 4 x 5) + ( 4 – 1) (5 – 1 ) + ( 4 – 2) (5 – 2 ) + ( 4 – 3) (5 – 3 ) + ( 4 – 4) (5 – 4 )

= 20 + 12 + 6 + 2 +0 = 40

Formula- 2

Here consider large value is n

i.e n = 5 and m = 4,  Now substitute these values in above formulas

= [ 4 x 1 x 5 / 2 ] + [ 4 x 5 x 9 / 6 ] 

= 10 + 30 = 40

Number of squares in given figure = 40

How many rectangles are there in the given figure

Count number of rectangles in the figure of  same number of rows and columns grid

( i.e Counting rectangles within a square )

Example – 4   How many rectangles are there in an 5 x 5  grid

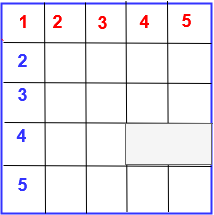
Solution: There are 5 rows and 5 columns in the above figure.

Let number of rows or columns ( n)=5

Here for finding the rectangles there are having two methods

Formula – 1

[n + ( n -1 ) + ( n -2 ) + ( n -3 ) + – – – – –  + ( n -n )]²

Now substitute the values of’  n‘ in the above formula

= [ 5 + (5 – 1 ) + (5 – 2 ) + (5 – 3 ) + (5 – 4 ) + (5 – 5) ]²

= [ 5 + 4 + 3+ 2 + 1 +0 ]²

= 15  x 15 = 225

Formula – 2

To count the number of rectangles within a square by using formula of

Now substitute the values of’  n‘ in the above formula

= [ 5 ( 5 + 1 ) /2 ] ²  =[ 5 x 6 / 2 ]²

= 15 ² = 225

Total number of rectangles in given figure = 225

Count number of rectangles in the figure of  ‘n’ number of rows and ‘m’ number of columns

( i.e Counting rectangles within a rectangle )

Example – 5  How many rectangles are there in an 4 x 5  grid

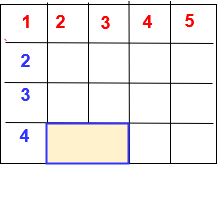
Solution:  There are 4 rows and 5 columns in the above figure.

Let number of rows ( n)=4 & number of columns (m) = 5

Here for finding the rectangles there having two methods

Formula – 1 ( Formula for finding number of rectangles in figure of  ‘n’ number of rows and ‘m’ is the number of columns)

[n + ( n -1 ) + ( n -2 ) + ( n -3 ) + – – – – –  + ( n -n )] x  [m + ( m -1 ) + (m -2 ) + (m-3 ) + – – – – –  + ( m -m )]

Now substitute the values of’  n‘ and ‘ m‘  in the above formula

= [ 4 + (4 – 1 ) + (4 – 2 ) + (4 – 3 ) + (4 – 4 )]  x [ 5 + (5 – 1 ) + (5 – 2 ) + (5 – 3 ) + (5 – 4 ) + (5 – 5) ]

= [ 4 +3 +2 +1 +0 ] x [ 5 + 4 + 3+ 2 + 1 +0 ]

= 10  x 15 = 150

Formula – 2  

 

Now substitute the values of’  n‘ and ‘ m‘  in the above formula

= 4 x 5 x 5 x 6 / 4 = 150

Total number of rectangles in given figure =  150

Related Articles

Count the number of triangles | Find the Number of triangles in the given figure

Unit Digit Problems with Solutions | How to Find Unit Digit of a Power Number

Number System | How to Find Total Number of Factors for Big Numbers Easily

Basic Concepts of number system in mathematics