In this page learn about Geometric Progression Tutorial – nth term of GP, sum of GP and geometric progression problems with solution for all competitive exams as well as academic classes.
Geometric Sequences Practice Problems | Geometric Progression Tutorial
Formulas and properties of Geometric progression
Geometric progression exercises with answers
Example – 1 : Write G.P if a = 128 and common ratio r = -1/2
Solution : General form of G.P = a, ar, ar2, ar3 . . . . . . .
128, -64, 32, -16, . . . . . . .
Formula for nth term G.P is an = arn-1
Example- 2: Find the 10th and nth term of the Geometric sequence 7/2, 7/4, 7/8, 7/16, . . . . . . .
Solution: Here a = 7/2 and common ratio = (7/4) / (7/2) = 1/2
Formula for nth term G.P is an = arn-1
10th term of given G.P = (7/2) x (1/2)9= (7/2) x (1/514) = 7/1024
nth term = (7/2) x (1/2)n-1 = 7 / 2n
Example- 3 The number 2048 is which term in the following Geometric sequence 2, 8, 32, 128, . . . . . . . . .
Solution: Here a = 2 and r = 4
nth term G.P is an = arn-1
⇒ 2048 = 2 x ( 4) n-1
⇒ 1024 =( 4) n-1
⇒ ( 4) 5 = ( 4) n-1
⇒ n = 6
Note: Given G.P is simple numbers. So we can find easily by direct multiplication upto required number.
Example – 4: Find the 15th term of a G.P Whose 8th term is 192 and the common ratio is ‘2’
Solution: Let first term of G.P is ‘a’ and common ratio r = 2
8th term of G.P is 192 So
⇒ 192 = a x (2)7
⇒ a = 192 / (2)7
Now 15th is
a15 = [ 192 / (2)7 ] (2) 14
a15 = 192 x 2 7 = 3 x 2 6 x 2 7 = 3 x 2 13
Example – 5: In a G.P first term is ‘1’ and 4th term is ‘ 27’ then find the common ration of the same.
Solution: Here a = 1 and a4 = 27 and let common ratio is ‘r’ . So
⇒ a4 = a r4-1
⇒ 27 = 1 r4-1 = r3
⇒ Common ratio = r = 3
Example – 6: Find ‘a’ so that a, a+2, a+6 are consecutive terms of a geometric progression.
Solution: If a1, a2, a3 , . . . . . . is a GP then
i.e Common ratio = r = a2 / a1 = a3 / a2 = a4 / a3 = . . . . .
So ⇒
⇒ a2 + 6a = a2 + 4 + 4a
⇒ a = 2
Example – 7 : If (a-b), (b-c), (c-a) are the consecutive terms of G.P then find (a +b + c)2
Solution: As per properties of Geometric Progression
⇒ commoon
⇒ b2 + c2 – 2bc = ac – a2 -bc + ba
⇒ a2 + b2 + c2 = ab + bc + ca —————– ( i )
Now take (a +b + c)2 as per algebraic formula
(a +b + c)2 = a2 + b2 + c2 + 2 (ab + bc + ca) —————– ( ii )
From the above two equations ( i ) & ( ii )
(a +b + c)2 = 3 (ab + bc + ca)
Example – 8: In a G.P 6th term is 24 and 13th term is 3/16 then find 20th term of the sequence.
Solution: Let first term is ‘a’ and common ratio is ‘r’
Here a6 = 24 ————- ( i) & a13 = 3/16 ————– ( ii)
⇒ a6 = a r6-1 & a13 = a r13-1
⇒ 24 = a r5 & 3/16 = a r12
⇒ r7 = 3 / 24 x 16 = 1 / (2)7
⇒ r = 1/2 ———– (iii)
from the above equations
⇒ a6 = 24 = a (1/2)5
⇒ a = 3 x 28
Now a20 = a r20-1
a20 = 3 x 28 x ( 1/2 )19 = 3 / 211
Example – 9: The 7th term of a G.P is eight times of fourth term. What will be the first term when its 5th is 48?
Solution:Let first term is ‘a’ and common ratio is ‘r’ for the given geometric sequence
Here given a7 = 8 x a4 and also a5 = 48
⇒ a r7-1 = 8 x a r4-1
⇒ r6 = 8 x r3
⇒ r = 2
Now take a5 = 48
⇒ a r5-1 = 48
⇒ a 24 = 48
⇒ a = 3
Example -11: Four geometric means are inserted between 1/8 and 128. Find second geometric mean.
Solution: Formula – The ‘n’ numbers G1, G2, G3, . . . . . . . Gn are said to be Geometric means in between ‘a’ and ‘b’. If a, G1, G2, G3, . . . . . . . Gn, b are in G.P.
So second geometric mean in sequence is
In the given sum a = 1/8 , n = 4 and b = 128
G2 = (1/8) ( 128 x 8)2/5
G2 = 2
Example-12: ‘x’ and ‘y’ are two numbers whose AM is 25 and GM is 7. Find the numbers
Solution: Here x’ and ‘y’ are two numbers then
Arithmetic mean = AM = (x+y)/2
Geometric Mean =GM =
So
x + y = 50 ————— ( i) & xy = 49 ———- (ii)
From the above equations the number can be 1 & 49
Application of geometric progression
Example – 1: If an amount ₹ 1000 deposited in the bank with annual interest rate 10% interest compounded annually, then find total amount at the end of first, second, third, forth and first years.
Solution: Here a = 1000 (staring of first year) and common ration = 1.1
So the total amount at the end of first, second, third, forth and first years will be in geometric sequence
At staring of 1st year – 1000
For the end of the 1st year – 1000 x 1.1 = 1100
For the end of the 2nd year – 1100 x 1.1 = 1210
For the end of the 3rd year – 1210 x 1.1 = 1331
For the end of the 4th year -1331 x 1.1 = 1464.1
For the end of the 5th year – 1464.1 x 1.1 = 1610.5
Example – 2: Salary of Robin, When his salary is ₹ 5,00,000 per annum for the first year and expected to receive yearly increment of 10%. Now find the Robin salary at staring of 5th year.
Solution: Here a = 5,00,000 and common ratio = 1.1
Robin salary at staring of 5th year i.e n = 5
Formula for nth term G.P is an = arn-1
a5 = 500000 x (1.1)4 = 500000 x 1.4641 = 7,32,050
Example – 3: The square is draw by joining the mid points of the sides of given square. A second square is drawn inside the second square in the same way second square is drawn inside the third square and this process continues upto 8th square. If a side of the first square is 32 cm then find the area of the first to eight square
Solution: Here area of the first square = 32 x 32 = 1024 cm2
Second square = 162 + 162 = 512 cm2 ( 1024/2 = 512)
Third square = 162 = 256 cm2 ( 512/2 = 256)
From the above, areas of the squares are in geometric progression
so remaining areas of squares are 128, 64, 32, 16 and 8 cm2
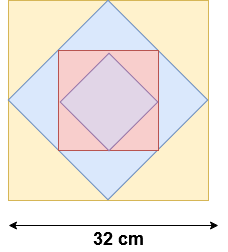
In the same way remaining areas of squares are 128 cm2, 64 cm2, 32 cm2, 16 cm2 and 8 cm2

Related Articles
Arithmetic Progression Formulas
Arithmetic Progression Questions with Solutions
Arithmetic Mean formula with Examples
Geometric Progression formulas
Geometric Progression Examples
Harmonic Progression formulas and examples
Relation Between arithmetic ,Geometric and Harmonic means






6 thoughts on “Geometric progression problems and solutions with Formulas and properties”
Francis
(August 5, 2021 - 8:00 pm)Very good site
sivaalluri
(August 7, 2021 - 5:31 am)Thanks
Ajayi Dele
(October 24, 2021 - 2:02 pm)Pls I don’t really know maths
Tony
(January 27, 2023 - 7:21 am)Please I really don’t know maths 🙄 help me
Oluyole
(October 30, 2021 - 11:11 am)I need alert from this site
Bashir Ibrahim
(June 9, 2022 - 9:00 am)Let my apologies for the solution of geometric progression