Different types of angles in Geometry | Mathematics Angles

In this section we know about definition of angle in geometry and its types of angles like Interior and Exterior of an angle, Zero Angle, Acute Angle, Right Angle, Obtuse angle, Straight Angle, Reflex Angle & Complete angle

What is Angle

An angle is formed when two rays originate from same end point. The two rays formed an angle are called ‘arms or ‘sides ‘ of the angle and the end point is called the vertex of the angle.

An angle is denoted by the symbol ” ∠ “

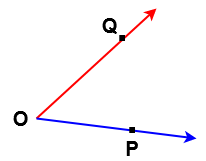
Here the rays OP, OQ from an angle denoted by ∠POQ or ∠QOP.

Sometimes, the above angle by written by the letter at the vertex of the angle. For example , in the above figure the angle ∠POQ is also denoted by “ ∠O ” or angle O

$definition of angle in geometry | different types of angles | all math tricks |$

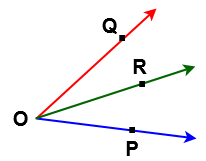
In the above figure angles are named as follows

∠POR , ∠POQ & ∠ROQ

The standard unit for measuring an angle is degree.

Degree is defined as 360^th part of one complete revolution.

One complete revolution is equal to 360 degree or 360^o

One degree is further divided into 60 equal parts. Each equal part is called one minute and it is written as 1′

1^o = 60′

One minute is further divided into 60 equal parts. Each equal part is called one second and it is written as 1″

1′ = 60″

Angles in Maths | Acute, Right, Obtuse, Straight, Reflex & Complete angle

Interior and Exterior of an angle

Interior of an angle : The part of the plane which is within the arms of an angle produced indefinitely is called the interior of the angle.

Exterior of the angle: The part of the plane which is outside the arms of an angle produced indefinitely is called the exterior of the angle.

For example:

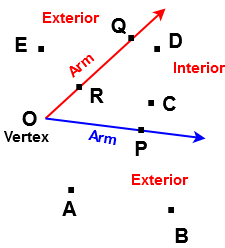
In the above figure all points in the plane of ∠POQ can be divided into three regions

On the angle : The points on the angle are P, Q & R

Interior of the angle : The points in the interior – C & D

Exterior of the angle : The points in the exterior – A, B & E

Types of Angles:

Zero Angle

The angle is formed by initial and final position of a ray coincide without making any revolution. Thus whose measure is O^o is called zero angle.

For example:

In the above figure ∠POQ = Zero angle = O^o

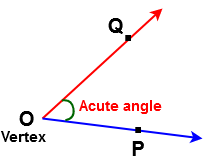
Acute Angle

The angle whose measure is less than 90^o is called an acute angle. It is also defined as ” An angle which is greater than zero angle bust less a right angle is called an acute angle.

For example 35^o , 40^o , 60^o , 70^o . . . . . etc are acute angles.

In the below figure ∠POQ is called acute angle.

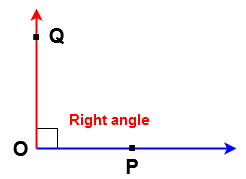
Right Angle

The right angle is defined as ” If the initial position of the ray OP is horizontal and it rotates to occupy vertical position OQ then we say that angle formed is a right angle .

Thus , the angle whose measure is 90^o is called right angle.

Obtuse angle

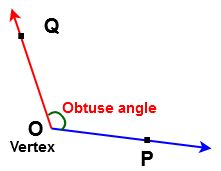
The angle whose measure is greater than 90^o but less than 180^o is called obtuse angle.

For example 95^o , 100^o , 120^o , 170^o . . . . . etc are Obtuse angle.

In the below figure ∠POQ is called Obtuse angle.

Straight Angle

The straight angle is formed when the initial and final position of a rotating ray opposite to each other.

The angle by two opposite rays OP and OQ is a straight angle since they form a straight line PQ and this is half of one complete angle.

Thus ∠POQ = 180^o = Straight angle.

Reflex Angle

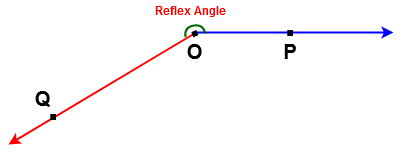
The angle whose measure is more than 180 o and less than 360o is called reflex angle.

For example: 200^o , 250^o , 300^o , 350^o . . . . etc are reflex angles.

In the below figure ∠POQ is called Reflex angle.

Complete angle

The angle is said to be complete angle, If an angle id formed by rotation ray, after making a complete revolution, coincides with the initial position.

Thus, the angle whose measure is 360^o is called complete angle.