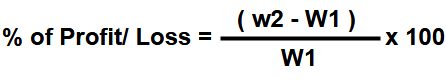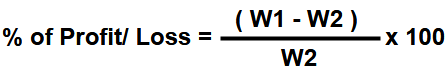Formulas for Profit and loss and practice sums | Exercise – 3
In Profit and Loss Exercise – I explained about the terminology with formulas and practice sums on Cost Price (CP), Selling price (SP), Profit (P), Loss(L), Gain , Gain percent.Profit percent and Loss percent.
In Profit and Loss Exercise – II explained about the terminology with formulas and practice sums on Mark Up, Marked price/ List Price, Discount, Discount Percentage & Successive discounts.
Now In this chapter covers remaining terminology with formulas and practice sums on Profit and Loss.
Direct Cost or Variable Cost :
This is the cost associated with direct selling of product/services. In other words, this is the cost that varies with every unit of the product sold. So the variable cost is a type of cost which varies according to the number of units.
Indirect Cost s or Fixed costs :
There are some types of costs that have to be incurred irrespective of the number of items sold and are called as fixed or indirect costs. So the fixed cost will not vary according to the number of units produced or sold.
For example the rent of the shop for the shopkeeper is fixed irrespective of his goods or product sold.
Semi-variable cost:
Some costs are such that they behave as fixed costs under normal circumstances but have to be increased when a certain level of sales figure is reached.
For example A trader sales increased such an extent that the trader need to take up additional storage room required to accommodate the increase in goods transactions. So the rent of the extra storage room becomes a part of the semi-variable cost.
Margin or Contribution per Unit :
The diffidence between the value of the selling price and the variable cost for the product is known as margin or contribution of the product.
This margin goes towards the recovery of the fixed costs incurred in selling the product cum services.
Break Even Point :
The break even point is defined as the volume of the sales at which there is no profit and no loss. In other words, the sales value in-terms of the number of units sold at which the company breaks even is called the break even point. This point is called break even sales.
For example A Rice trader take a shop for ₹6000 rent per month and arranged a sales boy for ₹9000 salary per month. Now the trader gets profit ₹30 per each rice bag sold. Then
Break Even Sales = Fixed costs / Margin per unit.
Fixed costs = 6000+ 9000 = 15000
Margin per unit = 30
Break Even Sales = 15000/30 = 500 bags
Hence the rice trader Breaks – Even on a monthly basis by selling 500 rice bags
Profit = ( Actual sales – break even sales ) x Contribution per unit.
Loss = ( Break even sales – Actual sales ) x Contribution per unit.
Chain Rules :
A sells an article to B at a profit of B sells it to C at a profit of and C sells it to D at a profit of . Then,
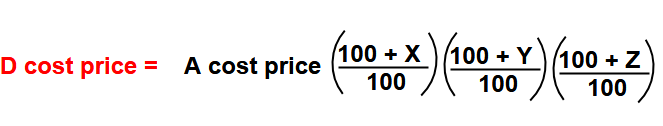Note : In this formula to be consider “+ve” sign for profit and “-ve” sign for loss.
Faulty Measure or Faulty Balances :
The seller gets profit while selling price more then cost price. Some dishonest sellers for getting more profit he will using some faulty balances and faulty measures.
The shopkeeper uses faulty balance of weight instead of “, but professes to sell his goods at cost price,
If the value comes ” +ve ” then it gives profit and the values comes ” -ve ” value then it incurred Loss.
The trader uses faulty measure of ” t “ units instead of units and sells his goods at a profit of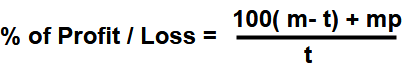 
If the value comes ” +ve ” then it gives profit and the values comes ” -ve ” value then it incurred Loss.
A shopkeeper cost price of articles is same as selling price of “n” articles,
Then profit/ loss percentage = [ (m – n) x 100 ] / n
If the value comes ” +ve ” then it gives profit and the values comes ” -ve ” value then it incurred Loss.
A trader purchases articles for cost of and sells articles for cost of “n” Then,
Then profit/ Loss percentage = [ (xn – my) 100 ] / my
If the value comes ” +ve ” then it gives profit and the values comes ” -ve ” value then it incurred Loss.
The trader an article is sold at a price of ” m” then trader loses a certain amount. If the article is sold at a price of , he gains the same amount. Then,
Cost price of the article = ( m + n) / 2.
Practice Sums related to above profit and loss formulas
Example – 1 : A shopkeeper adjusted his measuring balance faulty by 200gms more per 800gms of weight and he sold at cost price, Then find the profit percent for shopkeeper and also find loss% for costumer?
Answer : Here Cost price equal to sell price
The balance shows error 200gms more for 800gms weight, So actual weight 800gm and it sold to costumer as 1000gms. W1 = 800 and W2 = 1000 now the profit to shopkeeper
Profit percent = [ (1000- 800 ) /800 ] x 100
= 200 x 100 / 800 = 25%
W1 = 800 and W2 = 1000 now the loss percent to customer
Loss % = [ (800- 1000 ) /1000 ] x 100
= – 200 x 100 / 1000 = – 20% (“-ve ” value means its having loss)
So The shopkeeper gets profit 25% and the customer incurred loss of 20%
Example – 2 : A shopkeeper unknowingly measuring balance faulty by 200gms less per 1000gms of weight but he sold at 30% profit, Then find the profit/loss percent for shopkeeper?
Answer: The balance shows error 200gms less for 1000gms weight, So actual weight 1000gm and it sold to costumer as 800gms. W1 = 1000 and W2 = 800 now the profit to shopkeeper.
Loss percent = [ (800- 1000 ) /1000 ] x 100
= – 200 x 100 / 1000 = – 20% (“-ve ” value means its having loss)
Overall Profit / loss percent
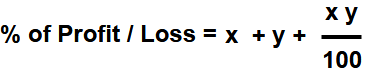Here x = -20 and y = 30 ( Here to be take “-ve” sign for loss and +ve sign for profit )
= -20 + 30 + ( – 20 x 30/100)
= -20 + 30 – 6
= + 4 %
Finally the shopkeeper gets 4% profit.
Example – 3 : A trader cost price of the 20 articles equal to selling price of 18 articles then find the profit / loss percent?
Answer : Here take m = 20 and n = 18
Then profit/ loss percentage = [ (m – n) x 100 ] / n
= ( 20 – 18 ) x 100 / 18
= 2 x 100 / 18 = (100/9)%
Profit percent = 11.11%.
Example – 4 : A trader cost price of the 20 articles for the cost of ₹ 100 and selling price of 18 articles for the cost of ₹120 then find the profit / loss percent?
Answer : Here take x = 20 and y = 100 ; m = 18 and n = 120
Then profit/ Loss percentage = [ (xn – my) 100 ] / my
= ( 20 x 120 – 18 x 100 ) x 100 / ( 18 x 100 )
=60000 / 1800 = + 33.33%
The trader gets profit 33.33%
For More practice sums with explanation on profit and loss chapter purpose go through the below link.
