Percentage formulas while increase and decrease percent of a number

Percentage formulas | percentage calculations with examples

Percentage calculation is one of the important part in mathematics. Percentage formulas very helpful to all competitive exams as well as in our daily life. In this artical provides different types of  formulas for percentage calculation with examples.

Type 1 : General Percent formulas.

Find X is what percent on Y ?

 

 

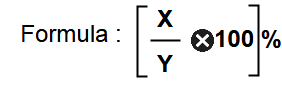
X is what percent greater than Y ?

 

 

$\mathrm{Find\; X}$is what percent lesser than Y ?

 

 

Examples for the above percentage formulas

Ex. 1 : 25 is what percent on 40 ?

solution : (25/40) x 100 = 62.5%

Ex. 2 : 25 is what percent less than 40 ?

solution : [(40-25)/40] x 100 = 37.5%

Ex. 3 : 50 is what percent greater than 40 ?

solution : [(50-40)/40] x 100 = 25%

Type 2 : Net change of a number while percentage increase or decrease.

Net change of a number while increased by $X\%$ and then again increased by Y$\%$.

 

 

Net change of a number while decreased by $X\%$ and then again decreased by Y$\%$.

 

The Net change of a number while increased by $X\%$ and then again decreased by Y$\%$.

 

 

Net change of a number while decreased by $X\%$ and then again increased by Y$\%$.

 

 

Hints:

1. Increase means ” + ”  sign and decreased means ” – ” sign . If net change is positive, it means final value  increased. If net change is negative, it means final value  decreased.
2. A number increases by  x $\%$ and then again decreases by $x\%$, (i.e same percent) then, net value always decreases by  (x / 10)²
3. If a number decreases by  x $\%$ and then again increases by $x\%$, (i.e same percent) then, net value always decreases by  (x / 10)²

Examples for the above percentage formulas

Ex.1 :  Find the net percent change of a number while it is increased by 20$\%$ and then again increased by 1$0\mathrm{\%\; ?}$

Solution : 20 + 10 + ( 20 x 10 /100) = 32%  increased.

Ex.2 :  Find the net value of a number  ” 60 “while it is increased by 25$\%$ and then again decreased by 15$\mathrm{\%\; ?}$

Solution : 25 – 15 – (25 x 15/100) = 25 – 15 – 3.75 = 6.25 %  ( increased )

= 60 + (60 x 6.25 %)  = 60 + [ 60 x (6.25/100)] = 60 + 3.75 = 63.75.

Ex.3 :  Find the net value of a number  ” 240 “while it is decreased by 30$\%$ and then again increased by 10$\mathrm{\%\; ?}$

Solution : -30 + 10 – (30 x 10/100) = – 30 + 10 – 3 = – 23 %  ( decreased )

= 240 – (240 x 23 %)  = 240 – [ 240 x (23/100)] = 240 – 55.2 = 184.8.

Ex.4 :  Find the net percent change of a number while it is decreased by 20$\%$ and then again decreased by 30$\mathrm{\%\; ?}$

Solution : – 20 – 30 + ( 20 x 30 /100) = -20 – 30 + 6% = -44% (decreased).

Ex.5 : Find the net change in revenue,  If price of a commodity decreases by $\mathrm{10}\%$ and again its price increases by $\mathrm{20}\mathrm{\%.}$

Solution :  – 10 + 20 – (10 x 20/100) = -10 + 20 -2 =  8 %

The final price of the commodity increased by 8%.

Ex.6 : Find the net change in revenue,  If price of a commodity decreases by $\mathrm{15}\%$ and again its price increases by 1$5\mathrm{\%.}$

Solution :   (15 / 10)²  = 2.25 %

The final price of the commodity decreased by 2.25%.

Type 3 : Net percent change in area of circle or square

If radius of a circle is increased by $x\%$, then its area is increased by

 

 

If radius of a circle is decreased by $x\%$, then its area is decreased by

 

 

Examples for the above percentage formulas

Ex.1 : Find the net change in area of a circle ,  If radius of the circle decreases by $\mathrm{20}\%$ and again its radius increases by 10$\mathrm{\%.}$

Solution :   – 20 + 10 – [(20 x 10) / 100)]  = -10 – 2 = -12% ( i.e radius decreased by 12% so change in radius 1- 0.12 = 0.88)

Area =    π x r²  = π x (0.88 r)²  =  0.7744 x  π x r²

So Area of the circle decreased by 100- 77.44 = 22.56%

Ex.2 : Find the net change in area of a circle ,  If radius of the circle increases by $\mathrm{30}\%$ and again decreases by 10$\mathrm{\%.}$

Solution :   30 – 10 – [(30 x 10) / 100)]  = 20 – 3 = -17% ( i.e radius increased by 17% so change in radius 1+0.17 = 1.17)

Area =    π x r²  = π x (1.17 r)²  = 1.3689 x  π x r²

So Area of the circle increased by 136.89 – 100 = 36.89%

Ex.3 : Find the net change in area of a square ,  If side of the square increases by $\mathrm{30}\%$.

Solution :  (2 x 30) + (30 x 30 /100) = 60 + 9 = 69%

So Area of the square increased by 69%

Ex.4 : Find the net change in area of a circle ,  If radius of the circle decreases by $\mathrm{18}\%$.

Solution :  – (2 x 18) + (18 x 18 /100) = – 36 +3.24 = – 32.73%.

So Area of the circle increased by 32.73%.

 

Math Tricks

Easy Addition and Subtraction Tricks | Shortcut Process for addition

Shortcuts for Multiplication of numbers | Easy way for Multiplications

Easiest way to find square of a 2 digit number | Shortcut trick for Square

Shortcut Methods for finding the Cube of a number | number cube tricks

Cube Root formula of Perfect Cubes of 1 to 100 | Cube root formula in math

Short Cut methods to square root calculation with examples

Shortcuts methods of Division math | Tips and tricks for math division

Hi friends Thanks for reading. I Hope you liked it. Give feed back, comments and please don’t forget to share it

---