Simple interest and Compound interest formulas with Online calculator

Online calculator for Simple interest and Compound interest with formulas and Examples

What is interest ( I )

The extra money, that will be paid or received for the use of the principal after a certain period is called the Total interest on the capital.

The interest calculated in two basis, they are

Simple Interest.
Compound Interest.

The Terminology involved in interest.

Creditor and Debtor :

The man who lends money is the Creditor and the man who borrows money is the Debtor.

Capital or Principal money ( P ):

The amount of money that is initially borrowed is called the Capital or Principal money.

Time ( N )

The period for which money is deposit

ed or borrowed is called Time.

Rate of Interest ( R )

It is the rate at which the interest is calculated and is always specified in percentage terms. i.e The interest of 1 year for every 100 called the interest rate per annul.

Amount ( A ):

The sum of the principal and the interest at the end of any time is called the Amount

Amount = Principal + Total Interest.

Simple Interest definition

It is calculated on the basis of a basic borrowed for the entire period at a particular rate of interest. The amount borrowed is the principal for the entire period of borrowing.

Formula for Simple interest ( S. I ) :

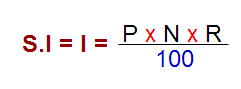
Where P = principle

N = Time in no. of years

R = rate of interest per annum

Amount ( A ) = P + I

Note: The rate of interest is normally specified in terms of annual rate of interest, In such a case we take the time 1 in years. However, If the rate of interest is specified in terms of 6-monthly rate, take time in terms of 6 months.

Illustrations on Simple interest for competitive exams:

Example : 1

Sum : Find the S.I on 900 for 3 years at 5% rate of interest per annum

Solution: P = 900, N= 3 , and R = 5 135

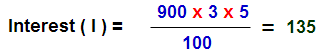
Example :2

Sum : Find the S.I and amount on 1800 for 3 years 4 months at 5 1/3% rate of interest per annum

Solution: P = 1800, N( to be in years) = [(3 x 12) + 4] / 12 = 10/3 , R = 5 1/3 = 16/3

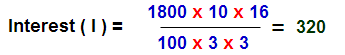
Amount = P + I = 1800 + 320 = 2120

Example :3

Sum : On what sum of money will the S.I for 5 years and 6 months at 3 1/3% per annum be 275 interest

Solution: P = ? , N( to be in years) = [(5 x 12) + 6] / 12 = 66/12 , R = 3 1/3 =10/3

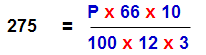
So P = 1500

Example :4

Sum : The simple interest on a sum of money is 25% of the principal , and the rate per annum is equal to the number of years. Find the rate of interest ?

Solution : Here S.I = 25% on principal

i.e I = 0.25 P

Rate of interest per annum = No. of years

i.e R = N

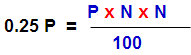
N² = 0.25 x 100

N =5 and R =5%

Example :5

Sum : The rate of interest for first 3 years is 10% per annum, for the next 4 years 7% per annum and for beyond years 5% per annum. If a man lent out 3000 for 10years. find the total interest.

Solution: For any amount

1st three years @ 10% rate of interest per annum

i.e S.I will be equal to 3 x 10 = 30%

Next four years @ 7% rate of interest per annum

i.e S.I will be equal to 4 x 7 = 28%

Remaining years @ 5% rate of interest per annum

i.e in this sum total 10 years so remaining years are 3 years so S.I will be equal to 3 x 5 = 15%

Total interest = 30 + 28 + 15 = 73%

Example :6

Sum : A sum of money double itself in 8 Years. Find the rate of interest per annum.

Solution: Here amount double itself means it is possible only at P = I and number of years is 8 ( N )

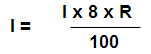
R = 100/8 = 12.5%

Example :7

Sum : The principal amount triple itself in in 10 years, In how many years it will be five times.

Solution : Here the amount (A) it equal to 3 times of Principal ( P) so I = 2P ans N= 10

so R = (100 x2 )/ 10 = 20%

In this sum required A = 5P i.e I = 4P and R = 20% than N= ?

N = 4 x 100 / 20 = 20 years

Example :8

Sum : In 4 years the principal 6000 amount to 8000 , In what time at the same rate of interest will be principal 525 to amount 700

Solution: Here Principal ( p ) = 6000 and Amount ( A ) = 8000

i.e I = A- P = 8000- 6000 = 2000 and N = 4 , R = ?

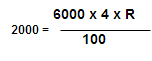
R = 2000 x 100/ (6000 x 4 )= 25/3 %

Now for 25/3% interest rate the principal (P) 525 is to be amount(A) 700

So I = A – P = 700- 525 = 175. and R = 25/3 % , N = ?

N = (175 x 100 x 3 )/(525 x 25) = 4 years

Compound Interest Definition

The interest of the previous period are added to the principal for the calculation of interest for next period . The period of time is depend upon agreement between creditor and debtor. It may be year or half yearly or quarterly with the condition that the interest accrued to the principal at a certain interval of time be added to the principal so that the total amount at the end of an interval becomes principal for the next interval.

Formulas for Compound Interest:

Let principal = P,

Time = N years

Rate of interest = r% per annum

Total amount at the end of the n years

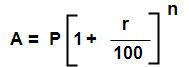
Case 1 : when compound interest is reckoned half – yearly.

I.e Let principal = P, Rate of interest = r% per annum , Time = N years

Than rate =( r/2)% half yearly and time 2n half year

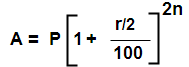
Case 2 : when compound interest is reckoned quarterly Let principal = P, Rate of interest = r% per annum , Time = N years

Than rate =( r/4)% quarterly and time 4n quarterly

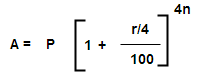
Take simple example for difference between simple and compound interest.

i.e A sum of 1000 at 10% per annum for 4 years. Find the simple interest and compound interest (Taken for C. I the interest being compounded in yearly)

Years	Simple Interest & Amount	Compound Interest & Amount
1^st Year	100 & 1100	100 & 1100
2^nd Year	100 & 1200	110 & 1210
3^rd Year	100 & 1300	121 & 1331
4^th year (Final Amount)	100 & 1400	133.1 & 1464.1

Note that the previous years’ interests are added to the original sum of 1000 to calculate the interest to be paid in the case of compound interest.

i.e in this cases the interest for the first interval is added to the principlal and this amount becomes the principal for the second interval, and so on.

Difference between the compound interest and simple interest

The difference between the compound interest and simple interest over the years is zero ( While in C.I is compounded by yearly)

The difference between the compound interest and simple interest over the two years is given by

Difference ( D ) = P x (R/100)²

The difference between the compound interest and simple interest over the three years is given by

Difference ( D ) = P x [R² (300 + R)/1000000]

Examples on Compound interest for competitive exams

Example : 1

Sum : Find the compound interest on principal 3000 at 20% rate of per annum for 1year & 6months by the interest being compounded by half yearly.

Solution: Here N = 2n = 2 x (18/12) = 3

R = r/2 = 20/2 = 10%

P = 3200

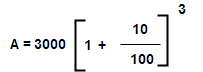
A = 3993

i.e Compound interest = A – P = 3993 – 3000 = 993

Example : 2

Sum : Find the Amount on principal 800000 at 10% rate of interest per annum for 2 years , the interest being compounded half yearly.

Solution : Here P = 800000, R = 10/2 = 5%, Time N = 2 x 2 = 4

So A = 800000 [ 1 + (5/100) ]⁴ = 972405

Example : 3

Sum : What amount does principal 1875 yield at 4% per annum at compound interest for 2 years.

Solution : Here P = 1875, R = 4 % and N=2

So A = 1875 [ 1 + (4/100) ]² =2028

Example : 4

Sum : What amount does principal 24000 yield at 5% per annum at compound interest for 3 years.

Solution : Here P = 24000, R = 5 % and N= 3

So A = 24000 [ 1 + (5/100) ]³ = 27783.

Example : 5

Sum : At what rate of interest % per annum C I will be principal 4000 to be amount 5324 in 3 years

Solution : Here P = 4000, A=5324 and N= 3 than R = ?

5324 = 4000 [ 1 + R/100]³

[ 1 + R/100]³ = (5324/4000) = 1331/1000 = (11/10)³

In the above equation is equal while R = 10 so R = 10%

(Note : In competitive exams simple logical thinking is require fast way of calculation)

Example : 7

Sum : The C. I on principal 10000 for 4 years is Rs 4641. Find the % rate of interest per annum

Solution: Here P = 10000, I= 4641, and N= 4 than R = ? than A = 10000+4641=14641

14641 = 10000 [ 1 + R/100]⁴

[ 1 + R/100]⁴= (14641/10000) = (11/10)⁴

In the above equation is equal while R = 10 so R = 10%

Example : 8

Sum : The C. I on principal 3000 for 2 years is Rs 630. Find the % rate of interest per annum

Solution: Here P = 3000, I= 630, and N= 2 than R = ?

now A =3000+630=3630

3630 =3000 [ 1 + R/100]²

[ 1 + R/100]²= (3630/3000) = 121/100= (11/10)²

In the above equation is equal while R = 10 so R = 10%

Example : 9

Sum : If the difference between the CI and SI on a certain sum of money is 72 at 12% rate of interest per annum for 2 years, than find the amount.

Solution : Here Difference between CI and SI ( D ) = 72 , R = 12% & N = 2 than P = ?

( D ) = P x (R/100)²

72 = P x ( 12/100)²
P = 72 x 100 x 100/ (12 x 12) =5000

So P = 5000

Example : 10

Sum : The difference S.I and C.I on principal 625 for 2 years is 4 than find the rate of interest per annum.

Solution : Here Difference between CI and SI ( D ) = 4 , R = ? & N = 2 than P = 625

( D ) = P x (R/100)²

4 = 625 x ( R/100)²

R² =4 x 100 x 100/ (625) =64

So R = 8%

Example : 11

Sum : The difference S.I and C.I on principal 15.20 for 3 years time @ 4% rate of interest per annum than find the principal.

Solution : Here Difference between CI and SI ( D ) = 15.20 , R = 4% & N = 3 than P = ?

Difference ( D ) = P x [R² (300 + R)/1000000]

15.20 = P x [4² (300 + 4)/1000000]

P = (152 x 100000) / (16 x 304) = 3125

Example : 12

Sum : A& B borrowing equal sums for 3 years @ 5% rate of interest for SI & CI respectively. At the time of repayment B has to pay 76.25 more than A than find the sum borrowed by the each person.

Solution : Here Difference between CI and SI ( D ) = 76.25 , R = 5% & N = 3 than P = ?

Difference ( D ) = P x [R² (300 + R)/1000000]

76.25 = P x [5² (300 + 5)/1000000]

P = (7625 x 10000) / (25 x 305) = 10000