Percentage calculation | Different shortcut methods to find out percentage

Percentage problems and solutions for aptitude

Percent means per hundred. Percentages are way of expressing hundredth. So ‘X ” percent means X per hundred or ” X/100 “. The concept of percentage mainly applies to ratios, and the percentage value of ratio is arrived at by multiplying by 100 the decimal values of ratio.

Percentage calculation plays very important role in the quantitative aptitude. Because some other topics in QA also depended on the percentage calculation.

Percentage formulas for different types of applications were already given the below like.

General Percent formulas | Net change of a number while percentage increase or decrease | Net percent change in area of circle or square.

In this page explained about some more examples with shortcut tricks on percentage calculation.

Example 1 : In trader gives successive discounts of 10%, 20% and 30% respectively. Then find percentage of the original coast price he will recover?

Solution : Its having the two methods and by using formula

Direct method : Take 100

100 x (100-10)% = 90 ( 10% discount ).

90 x (100 – 20)% = 72 ( 20% discount ).

72 x ( 100-30) % = 50.4 ( 30% discount ).

Hence overall discount 49.6 % and the answer is 50.4%.

By using formula :

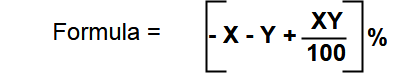
Take 10% and 20% discounts

i.e -10 – 20 + (10 x 20 /100 ) = -28% ( i.e Negative sign means 28% discount )

Take 28% and 30% discounts

i.e -30 – 28 + (30 x 28 /100 ) = – 49.6% ( i.e overall discount 49.6 % discount)

Our final answer is 50.4 % ( 100%-49.6% = 50.4%).

Example 2 : A person salary increased 20% and then deceased by 20%. What is the net percentage change in his salary?

Solution : Here remember one tip ” The net percent always decreased when same percent increased then decreased or same percent decreased then increased”.

By using formula (x / 10)²Here take x = 20

= (20 / 10)² = 4 % decreased.

Example 3 : ” A’s ” salary is 50% more than B’s salary. By what percent is B ‘s salary less than A’s salary?

Sol: Take B’s salary 100 then A’s salary is 150. ( Due to 50% more ).

Now using the formula

= (1/3) x 100 = 33.33%

So B ‘s salary 33.33% less than A’s salary.

Example 4 : The length and the breadth of a rectangle are changed by +20% and by -10% respectively. What is the percentage change in the area of the rectangle?

Sol : Direct method

( 100 + 20) x ( 100 – 10) = 120 x 90 = 108%.

So area increased by 8%

Now by using formula

= 20 – 10 – 2 = 8% ( here comes positive value so it will be increased)

So area increased by 8%.

Example 5 : A’s salary is 30% lower than B’s salary, which is 20% lower than C,s salary. By how much percent is C’s salary more than A’s salary?

Here Take C’s salary 100 then B’s salary 100 x ( 100-20)% = 80

Now A’s salary 80 x (100-30)% = 80 x 70% = 56.

Now using the formula = X is what percent greater than Y ( here x = 100 and y = 56 ) $y$

[ (100-56) / 56 ] x 100 = 44 x 100 / 56 = 78.57%

So C salary 78.57% more than A’s salary.

For the above sum we can using one shortcut method

Lower means take negative sign for for 30% and 20%.

i. e -30 -20 + (30 x 20 / 100 ) = -44%

So A’s salary 44% less than C salary. If take C’ s salary 100 than A’s salary having 56.

Example 6 : The cost of manufacturing of a medicine is made up of four components A, B , C and D which have ratio of 4 : 3 : 1 : 6 respectively. If there are respective changes in the cost of +20% , -10% , -30% and +30%, then what would be the percentage change in cost.

Solution: Here we using one shortcut i.e + 20% = 1.2 , -10% = 0.9 , -30% = 0.7 , +30% = 1.3

Assume the ratio value for single medicine = 4 + 3 + 1 + 6 = 14

Now calculate the new cost for the medicine = (4 x 1.2) + (3 x 0.9) + (1 x 0.7) + (6 x 1.3)

= 4.8 + 2.7 + 0.7 + 7.8 = 16.

Now calculate the percentage change

= [ (16-14) / 14 ] x 100 =2 x 100 / 14 = 14.29%.

Example 7 : 30% of a number when subtracted from 91, gives the number itself. .Find the number?

Sol: Take the number ” X ” . 30% of ‘”X ” is 0.3X

Now 0.3X subtracted from 91 then comes ” X”

i.e 91 – 0.3X = X

X = 70.

Example 8 : Tom’s salary is 60% more than Ramki’s salary. Tom got a raise of 50% on his salary while Ramki got a raise of 20% on his salary. By what percent is Tom’s salary more than Ramki’s salary ?

Sol: Take Ramki’s salary 100 then Tom’s salary having 160.

Tom raise in his salary 50% . So Tom’s salary = 160 x 1.5 = 240.

Ramki raise in his salary 20% . So Ramki’s salary = 100 x 1.2 = 120.

Now calculate 240 what percent more than 120

= [ (240-120) / 120 ] x 100 = 120 x 100 / 120 = 100%.

Example 9 : If 65 % of ” N ” = 13% of ” M”, then find the value of “N” if “M” = 1000.

Sol: 65 % of ” N means 0.65N and 13% of ” M” means 0.13M

So if M = 1000 then

0.65 x N = 0.13 x 1000

N = 200.

Example 10 : The difference of two numbers is 40% of the large number. If the smaller number is 120, then find the large number?

Sol: Take large number ” x ” and smaller number “y ‘

According to given logic.

The difference of “x” and “y ” is 40% of the” x”.

x – y = 0.4x

Here take y = 120 then x = 200.

Example 11 : The price per unit of article decreases by 20%. By what percentage should the consumption be increased such that expenditure remain the same?

Sol: Using the formula [ x / (100- x) ] x 100

Here x = 20%

So [ 20 / (100- 20) ] x 100 = 25%

Example 12 : A person spends 25% of his salary on food , 15% on house rent, 38% on miscellaneous. If the savings at the end of a month is $880, then find his total salary?

Sol: Take total salary = X

then X = 0.25X + 0.15X + 0.38X + 880

X – 0.78X = 880

X = $4000.